题目内容
(本小题满分16分)
已知数列 和
和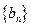 ,对一切正整数n都有:
,对一切正整数n都有:
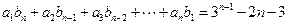 成立.
成立.
(Ⅰ)如果数列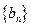 为常数列,
为常数列,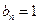 ,求数列
,求数列 的通项公式;
的通项公式;
(Ⅱ)如果数列 的通项公式为
的通项公式为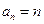 ,求证数列
,求证数列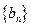 是等比数列.
是等比数列.
(Ⅲ)如果数列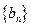 是等比数列,数列
是等比数列,数列 是否是等差数列?如果是,求出这个数列的通项公式;如果不是,请说明理由.
是否是等差数列?如果是,求出这个数列的通项公式;如果不是,请说明理由.
已知数列
 和
和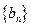 ,对一切正整数n都有:
,对一切正整数n都有: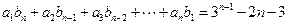 成立.
成立.(Ⅰ)如果数列
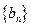 为常数列,
为常数列,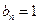 ,求数列
,求数列 的通项公式;
的通项公式;(Ⅱ)如果数列
 的通项公式为
的通项公式为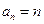 ,求证数列
,求证数列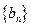 是等比数列.
是等比数列.(Ⅲ)如果数列
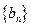 是等比数列,数列
是等比数列,数列 是否是等差数列?如果是,求出这个数列的通项公式;如果不是,请说明理由.
是否是等差数列?如果是,求出这个数列的通项公式;如果不是,请说明理由.(Ⅰ)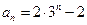 .
.
(Ⅱ)数列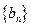 是4为首项,公比为3的等比数列.
是4为首项,公比为3的等比数列.
(Ⅲ)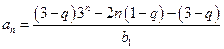 …
…
若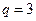 时,
时,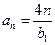 ,数列
,数列 为等差数列.
为等差数列.
若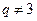 时,∵a2-a1≠a3-a2 ,
时,∵a2-a1≠a3-a2 ,
∴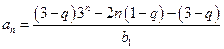 ,不是等差数列.
,不是等差数列.
故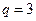 时,数列
时,数列 为等差数列;
为等差数列;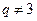 时数列
时数列 不为等差数列……16分
不为等差数列……16分
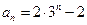 .
. (Ⅱ)数列
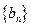 是4为首项,公比为3的等比数列.
是4为首项,公比为3的等比数列. (Ⅲ)
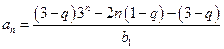 …
…若
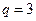 时,
时,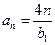 ,数列
,数列 为等差数列.
为等差数列.若
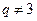 时,∵a2-a1≠a3-a2 ,
时,∵a2-a1≠a3-a2 ,∴
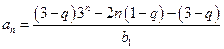 ,不是等差数列.
,不是等差数列.故
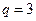 时,数列
时,数列 为等差数列;
为等差数列;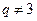 时数列
时数列 不为等差数列……16分
不为等差数列……16分 (本小题满分16分)
(Ⅰ)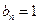 ,由已知得:
,由已知得: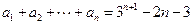 ,
,
将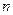 用
用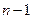 迭代得:
迭代得: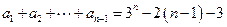 .(
.(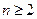 )
)
两式相减得: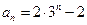 ,当
,当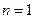 时,适合
时,适合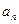
∴数列 的通项公式为
的通项公式为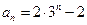 . ………………4分
. ………………4分
(Ⅱ)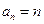 ,由已知得:
,由已知得: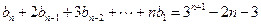 ,
,
将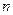 用
用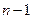 迭代得:
迭代得: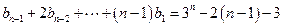 .(n≥2)
.(n≥2)
两式相减得: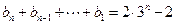 , ………………………7分
, ………………………7分
将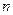 用
用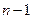 迭代得:
迭代得: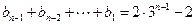 .
.
两式相减得: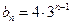 ,经检验
,经检验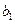 也适合.
也适合.
所以数列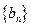 的通项公式为
的通项公式为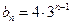 .
.
故数列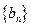 是4为首项,公比为3的等比数列. ………………10分
是4为首项,公比为3的等比数列. ………………10分
(Ⅲ)设数列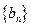 的首项为
的首项为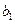 ,公比为
,公比为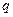 ,由已知得:
,由已知得:
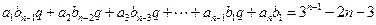
即: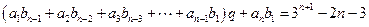
即:
所以: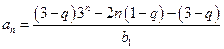 ………………………13分
………………………13分
若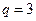 时,
时,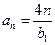 ,数列
,数列 为等差数列.
为等差数列.
若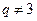 时,∵a2-a1≠a3-a2 ,
时,∵a2-a1≠a3-a2 ,
∴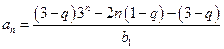 ,不是等差数列.
,不是等差数列.
故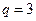 时,数列
时,数列 为等差数列;
为等差数列;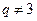 时数列
时数列 不为等差数列……16分
不为等差数列……16分
(Ⅰ)
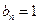 ,由已知得:
,由已知得: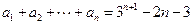 ,
,将
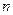 用
用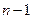 迭代得:
迭代得: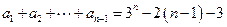 .(
.(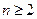 )
)两式相减得:
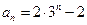 ,当
,当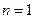 时,适合
时,适合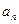
∴数列
 的通项公式为
的通项公式为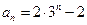 . ………………4分
. ………………4分(Ⅱ)
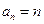 ,由已知得:
,由已知得: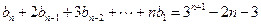 ,
,将
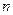 用
用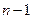 迭代得:
迭代得: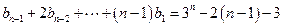 .(n≥2)
.(n≥2)两式相减得:
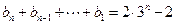 , ………………………7分
, ………………………7分 将
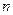 用
用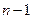 迭代得:
迭代得: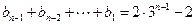 .
.两式相减得:
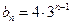 ,经检验
,经检验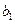 也适合.
也适合.所以数列
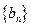 的通项公式为
的通项公式为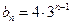 .
.故数列
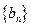 是4为首项,公比为3的等比数列. ………………10分
是4为首项,公比为3的等比数列. ………………10分(Ⅲ)设数列
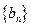 的首项为
的首项为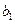 ,公比为
,公比为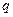 ,由已知得:
,由已知得: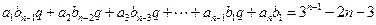
即:
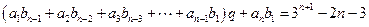
即:

所以:
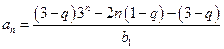 ………………………13分
………………………13分若
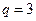 时,
时,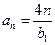 ,数列
,数列 为等差数列.
为等差数列.若
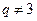 时,∵a2-a1≠a3-a2 ,
时,∵a2-a1≠a3-a2 ,∴
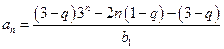 ,不是等差数列.
,不是等差数列.故
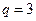 时,数列
时,数列 为等差数列;
为等差数列;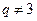 时数列
时数列 不为等差数列……16分
不为等差数列……16分 
练习册系列答案
相关题目
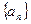 的前
的前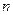 项和为
项和为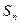 ,方程
,方程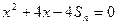 有一根为
有一根为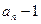
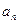 .
.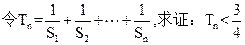 .
.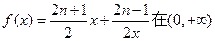 上的最小值是
上的最小值是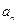 (
(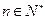 ).
).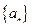 的通项公式;
的通项公式;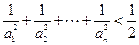 ;
;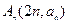 中,是否存在两点
中,是否存在两点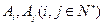 使直线
使直线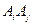 的斜率为1?若存在,求出所有数对
的斜率为1?若存在,求出所有数对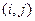 ,若不存在,说明理由.
,若不存在,说明理由.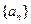 满足
满足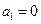 ,
,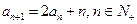 .
.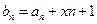 ,是否存在实数
,是否存在实数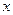 ,使得
,使得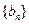 是等比数列;
是等比数列;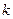 ,使得
,使得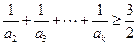 成立?若存在,求出
成立?若存在,求出 的前n项和为
的前n项和为 ,若
,若 等于( )
等于( )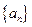 为等差数列,公差
为等差数列,公差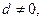
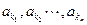 恰为等比数列,若
恰为等比数列,若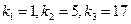 ,则
,则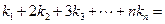 __ ▲ __.
__ ▲ __.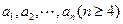 是各项均不为零的等差
是各项均不为零的等差 数列,且公差
数列,且公差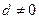 .设
.设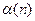 是将此数列删去某一项得到的数列(按原来的顺序)为等比数列的最大的
是将此数列删去某一项得到的数列(按原来的顺序)为等比数列的最大的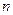 值,则
值,则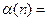
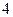 B.
B.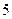
 C.
C. D.
D.
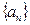 中,有
中,有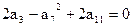 ,数列
,数列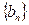 是等比数列,且
是等比数列,且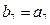 则
则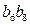 =" ( " )
=" ( " )