题目内容
生产A,B两种元件,其质量按测试指标划分为:指标大于或等于82为正品,小于82为次品,现随机抽取这两种元件各100件进行检测,检测结果统计如下:
| 测试指标 | [70,76) | [76,82) | [82,88) | [88,94) | [94,100] |
| 元件A | 8 | 12 | 40 | 32 | 8 |
| 元件B | 7 | 18 | 40 | 29 | 6 |
(1)试分别估计元件A、元件B为正品的概率;
(2)生产一件元件A,若是正品可盈利50元,若是次品则亏损10元;生产一件元件B,若是正品可盈利100元,若是次品则亏损20元,在(1)的前提下:
①求生产5件元件B所获得的利润不少于300元的概率;
②记X为生产1件元件A和1件元件B所得的总利润,求随机变量X的分布列和数学期望.
解:(1)由题可知,元件A为正品的概率为 ,元件B为正品的概率为
,元件B为正品的概率为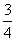 .
.
(2)①设生产的5件元件中正品件数为x,则有次品5-x件,由题意知100x-20(5-x)≥300得到x=4,5,设“生产5件元件B所获得的利润不少于300元”为事件C,则P(C)
②随机变量X的所有取值为150,90,30,-30,
则P(X=150)= ×
×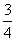 =
=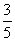 ,
,
P(X=90)= ×
×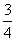 =
= ,
,
P(X=30)= ×
×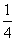 =
= ,
,
P(X=-30)= ×
×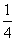 =
= ,
,
所以X的分布列为:
| X | 150 | 90 | 30 | -30 |
| P |
|
|
|
|

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案
相关题目
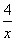 是定义在集合M=
是定义在集合M=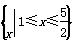 上的两个函数.对任意的x∈M,存在常数x0∈M,使得f(x)≥f(x0),g(x)≥g(x0),且f(x0)=g(x0).则函数f(x)在集合M上的最大值为( )
上的两个函数.对任意的x∈M,存在常数x0∈M,使得f(x)≥f(x0),g(x)≥g(x0),且f(x0)=g(x0).则函数f(x)在集合M上的最大值为( )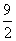 B.4
B.4 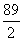
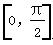 时,f(x)=xsin x,若a=f(cos 1),b=f(cos 2),c=f(cos 3),则a,b,c的大小关系为( )
时,f(x)=xsin x,若a=f(cos 1),b=f(cos 2),c=f(cos 3),则a,b,c的大小关系为( ) 的平面点集中随机取一点M(x0,y0),设事件A=“y0<2x0”,那么事件A发生的概率是( )
的平面点集中随机取一点M(x0,y0),设事件A=“y0<2x0”,那么事件A发生的概率是( )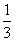 D.
D.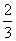
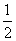 ,则a=________.
,则a=________.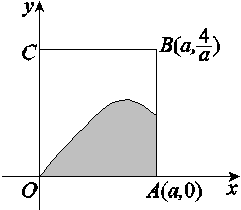
 的不同值的个数是( )
的不同值的个数是( )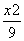 +
+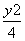 =1的两个焦点,P为椭圆上一点,已知P,F1,F2是一个直角三角形的三个顶点,且|PF1|>|PF2|,则
=1的两个焦点,P为椭圆上一点,已知P,F1,F2是一个直角三角形的三个顶点,且|PF1|>|PF2|,则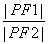 的值为( )
的值为( )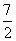 C.2或
C.2或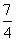
 的方程
的方程 有负实数根,则
有负实数根,则 ________
________