题目内容
证明:
(1)若f(x)=ax+b,则f(
)=
;
(2)若g(x)=x2+ax+b,则g(
)≤
.
(1)若f(x)=ax+b,则f(
| x1+x2 |
| 2 |
| f(x1)+f(x2) |
| 2 |
(2)若g(x)=x2+ax+b,则g(
| x1+x2 |
| 2 |
| g(x1)+g(x2) |
| 2 |
考点:函数的值
专题:函数的性质及应用
分析:(1)由已知条件利用函数性质能证明f(
)=
.
(2)由已知条件,利用函数性质能证明g(
)≤
.
| x1+x2 |
| 2 |
| f(x1)+f(x2) |
| 2 |
(2)由已知条件,利用函数性质能证明g(
| x1+x2 |
| 2 |
| g(x1)+g(x2) |
| 2 |
解答:
证明:(1)∵f(x)=ax+b,
∴f(
)=a•
+b
=
=
.
(2)∵g(x)=x2+ax+b,
∴g(
)=(
)2+a(
)+b
=
+
+
≤
=
.
∴g(
)≤
.
∴f(
| x1+x2 |
| 2 |
| x1+x2 |
| 2 |
=
| (ax1+b)+(ax2+b) |
| 2 |
=
| f(x1)+f(x2) |
| 2 |
(2)∵g(x)=x2+ax+b,
∴g(
| x1+x2 |
| 2 |
| x1+x2 |
| 2 |
| x1+x2 |
| 2 |
=
| x12+x22+2x1x2 |
| 4 |
| a(x1+x2) |
| 2 |
| 2b |
| 2 |
≤
| (x12+ax1+b)+(x22+ax2+b) |
| 2 |
=
| g(x1)+g(x2) |
| 2 |
∴g(
| x1+x2 |
| 2 |
| g(x1)+g(x2) |
| 2 |
点评:本题考查等式和不等式的证明,是基础题,解题时要注意函数性质的合理运用.

练习册系列答案
相关题目
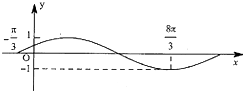 将函数y=sinx图象上点的横坐标扩大到原来的m倍,纵坐标保持不变,再向左平移n个单位得到如图所示函数的图象,则m,n可以为( )
将函数y=sinx图象上点的横坐标扩大到原来的m倍,纵坐标保持不变,再向左平移n个单位得到如图所示函数的图象,则m,n可以为( )A、m=2,n=
| ||
B、m=2,n=
| ||
C、m=4,n=
| ||
D、m=4,n=
|
已知随机变量ξ服从正态分布N(2,δ2),p(ξ<4)=0.84,则P(2<ξ<4)=( )
| A、0.68 | B、0.34 |
| C、0.17 | D、0.16 |
已知a>1,e=2.71828…是自然对数的底数,若函数y=logax与y=ax的图象与直线y=x相切于同一点,则a=( )
| A、ee | ||
| B、e2 | ||
| C、e | ||
D、e
|
若k∈R,则“-3<k<3”是“方程
-
=1表示双曲线”的( )
| x2 |
| k-3 |
| y2 |
| k+3 |
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
若直线ax+2y+1=0与直线x+y-2=0互相垂直,则实数a=( )
| A、1 | ||
| B、-2 | ||
C、-
| ||
D、-
|