Question

8．某种新产品投放市场一段时间后，经过调研获得了时间x（天数）与销售单价y（元）的一组数据，且做了一定的数据处理（如表），并作出了散点图（如图）．

$\overline{x}$	$\overline{y}$	$\overline{w}$	$\sum_{i=1}^{10}（{x}_{i}-\overline{x}）^{2}$	$\sum_{i=1}^{10}（{w}_{i}-\overline{w}）^{2}$	$\sum_{i=1}^{10}（{x}_{i}-\overline{x}）（{y}_{i}-\overline{y}）$	$\sum_{i=1}^{10}（{w}_{i}-\overline{w}）（{y}_{i}-\overline{y}）$
1.63	37.8	0.89	5.15	0.92	-20.6	18.40

表中w_i=$\frac{1}{{x}_{i}}$，$\overline{w}$=$\frac{1}{10}$$\sum_{i=1}^{10}{w}_{i}$．
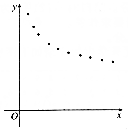（Ⅰ）根据散点图判断，$\widehat{y}$=$\widehat{a}$+$\widehat{b}$x与$\widehat{y}$=$\widehat{c}$+$\frac{\widehat{d}}{x}$哪一个更适宜作价格y关于时间x的回归方程类型？（不必说明理由）
（Ⅱ）根据判断结果和表中数据，建立y关于x的回归方程；
（Ⅲ）若该产品的日销售量g（x）（件）与时间x的函数关系为g（x）=$\frac{-100}{x}$+120（x∈N^*），求该产品投放市场第几天的销售额最高？最高为多少元？
附：对于一组数据（u₁，v₁），（u₂，v₂），（u₃，v₃），…，（u_n，v_n），其回归直线v=α+βu的斜率和截距的最小二乘估计分别为$\widehat{β}$=$\frac{\sum_{i=1}^{n}（{v}_{i}-\overline{v}）（{u}_{i}-\overline{u}）}{\sum_{i=1}^{n}（{u}_{i}-\overline{u}）^{2}}$，$\widehat{α}$=$\overline{v}$-$\widehat{β}$$\overline{u}$．

Answer 1

分析 （I）根据散点图的大体分布是否成直线分布判断；
（II）根据回归系数公式计算y关于w的线性回归方程，再转化为y关于x的回归方程；
（III）求出日销售额，利用二次函数的性质求出结论．

解答 解：（Ⅰ）由散点图可以判断$\widehat{y}$=$\widehat{c}$+$\frac{\widehat{d}}{x}$适合作作价格y关于时间x的回归方程类型；
（Ⅱ）令w=$\frac{1}{x}$，先建立y关于w的线性回归方程，由于d=$\frac{18.40}{0.92}$=20，∴c=37.8-20×0.89=20，
∴y关于w的线性方程为y=20+20w，
∴y关于x的线性方程为y=20+$\frac{20}{x}$；
（Ⅲ）日销售额h（x）=g（x）（20+$\frac{20}{x}$）=-200（$\frac{10}{x}$-12）（$\frac{1}{x}$+1）=-2000[（$\frac{1}{x}$-$\frac{1}{10}$）²-12.1]，
∴x=10时，h（x）有最大值2420元，
即该产品投放市场第10天的销售额最高，最高为2420元．

点评 本题考查了线性回归方程的求解及数值预测，函数的最值，属于中档题．