题目内容
17.已知直线2x+3y+6=0与圆x2+y2+2x-6y+m=0(其圆心为点C)交于A,B两点,若CA⊥CB,求实数m的值.分析 确定圆心与半径,利用CA⊥CB,可得圆心到直线的距离d=$\frac{\sqrt{2}}{2}$r,即可求实数m的值.
解答 解:圆x2+y2+2x-6y+m=0可化为圆(x+1)2+(y-3)2=-m+10,圆心坐标为(-1,3),半径为$\sqrt{10-m}$
∵CA⊥CB,
∴圆心到直线的距离d=$\frac{|-2+9+6|}{\sqrt{4+9}}$=$\frac{\sqrt{2}}{2}$•$\sqrt{10-m}$
∴m=-16.
点评 本题考查直线与圆的位置关系,考查点到直线距离公式的运用,考查学生的计算能力,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
8.己知抛物线x2=2ay(a为常数)的准线经过点(1,-1),则抛物线的焦点坐标为( )
| A. | (-1,0) | B. | (1,0) | C. | (0,-1) | D. | (0,1) |
9.圆C:x2+y2=1,直线l:y=kx+2,直线l与圆C交与A,B,若|$\overrightarrow{OA}$$+\overrightarrow{OB}$|<|$\overrightarrow{OA}$$-\overrightarrow{OB}$|(其中O为坐标原点),则k的取值范围是( )
| A. | (0,$\sqrt{7}$) | B. | (-$\sqrt{7}$,$\sqrt{7}$) | C. | ($\sqrt{7}$,+∞) | D. | ($-∞,-\sqrt{7}$)$∪(\sqrt{7,}+∞)$ |
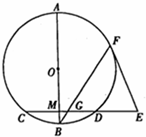 如图,AB是圆O的直径,弦CD⊥AB于点M,E是CD延长线上一点,AB=10,CD=8,3ED=4OM,EF切圆O于F,BF交CD于G.
如图,AB是圆O的直径,弦CD⊥AB于点M,E是CD延长线上一点,AB=10,CD=8,3ED=4OM,EF切圆O于F,BF交CD于G.