题目内容
6.已知极点与原点重合,极轴与x轴的正半轴重合,若曲线C1的极坐标方程为:ρ=2sinθ,曲线C2的参数方程为:$\left\{\begin{array}{l}{x=2cosθ}\\{y=\frac{2\sqrt{3}}{3}sinθ}\end{array}\right.$(θ为参数),曲线C1与C2交于M,N两点,求M,N两点间的距离.分析 求出曲线C1的直角坐标方程和曲线C2的普通方程,联立方程组,求出M,N点的坐标,由此能求出|MN|的长.
解答 解:∵曲线C1的极坐标方程为:ρ=2sinθ,
∴ρ2=2ρsinθ,
∴曲线C1的直角坐标方程为:x2+y2-2y=0,
∵曲线C2的参数方程为:$\left\{\begin{array}{l}{x=2cosθ}\\{y=\frac{2\sqrt{3}}{3}sinθ}\end{array}\right.$(θ为参数),
∴曲线C2的普通方程为$\frac{{x}^{2}}{4}+\frac{3{y}^{2}}{4}$=1,
联立$\left\{\begin{array}{l}{{x}^{2}+{y}^{2}-2y=0}\\{\frac{{x}^{2}}{4}+\frac{3{y}^{2}}{4}=1}\end{array}\right.$,得y2+y-2=0,
解得y=1或y=-2,∴M(-1,1),N(1,1),
∴|MN|=$\sqrt{(1+1)^{2}+(1-1)^{2}}$=$\sqrt{2}$.
点评 本题考查两点间距离的求法,是基础题,解题时要认真审题,注意极坐标方程和直角坐标方程互化公式的合理运用.

练习册系列答案
 寒假天地重庆出版社系列答案
寒假天地重庆出版社系列答案
相关题目
20.下列不能产生随机数的是( )
| A. | 抛掷骰子试验 | |
| B. | 抛硬币 | |
| C. | 计算器 | |
| D. | 正方体的六个面上分别写有1,2,2,3,4,5,抛掷该正方体 |
18.二次函数y=-x2+4x一3的最大值为( )
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
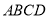 和直角梯形
和直角梯形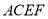 所在的平面互相垂直,其中
所在的平面互相垂直,其中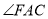 为直角,
为直角,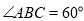 ,
,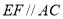 ,
,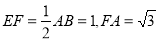 .
.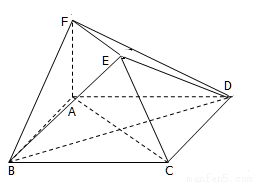
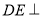 平面
平面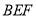 ;
;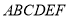 的体积.
的体积.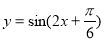 的图象向右平移
的图象向右平移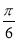 个单位,再纵坐标不变,横坐标变为原来的2倍,所得新图象的函数解析式是( )
个单位,再纵坐标不变,横坐标变为原来的2倍,所得新图象的函数解析式是( )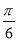 ) D.y=sin(x﹣
) D.y=sin(x﹣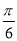 )
)