题目内容
1.设△ABC的内角A,B,C所对的边分别为a,b,c,满足$\frac{\sqrt{2}a-b}{c}$=$\frac{cosB}{cosC}$.(1)求角C的大小;
(2)设函数f(x)=cos(2x+C),将f(x)的图象向右平移$\frac{π}{4}$个单位长度后得到函数g(x)的图象,求函数g(x)在区间[0,$\frac{π}{3}$]上的值域.
分析 (1)由正弦定理和和差角的三角函数可得cosC,可得C值;
(2)由函数图象变换可得g(x)=cos(2x-$\frac{π}{4}$),由x∈[0,$\frac{π}{3}$]和三角函数的值域可得.
解答 解:(1)∵$\frac{\sqrt{2}a-b}{c}$=$\frac{cosB}{cosC}$,∴由正弦定理可得$\frac{\sqrt{2}sinA-sinB}{sinC}$=$\frac{cosB}{cosC}$,
∴$\sqrt{2}$sinAcosC-sinBcosC=cosBsinC,即$\sqrt{2}$sinAcosC=sinBcosC+cosBsinC
∴$\sqrt{2}$sinAcosC=sin(B+C)=sinA,sinA≠0,
同除以sinA变形可得cosC=$\frac{\sqrt{2}}{2}$,
∵C为三角形内角,∴C=$\frac{π}{4}$;
(2)由(1)和题意可得f(x)=cos(2x+$\frac{π}{4}$),
将f(x)的图象向右平移$\frac{π}{4}$个单位长度后得到函数g(x)的图象,
∴g(x)=cos[2(x-$\frac{π}{4}$)+$\frac{π}{4}$)]=cos(2x-$\frac{π}{4}$),
∵x∈[0,$\frac{π}{3}$],∴2x-$\frac{π}{4}$∈[-$\frac{π}{4}$,$\frac{5π}{12}$],
∴当2x-$\frac{π}{4}$=$\frac{5π}{12}$即x=$\frac{π}{3}$时,函数取最小值cos$\frac{5π}{12}$=cos($\frac{π}{4}$+$\frac{π}{6}$)
=$\frac{\sqrt{2}}{2}×\frac{\sqrt{3}}{2}-\frac{\sqrt{2}}{2}×\frac{1}{2}$=$\frac{\sqrt{6}-\sqrt{2}}{4}$;
当2x-$\frac{π}{4}$=0即x=$\frac{π}{8}$时,函数取最大值1,
故所求值域为:[$\frac{\sqrt{6}-\sqrt{2}}{4}$,1]
点评 本题考查三角函数图象变换,涉及设三角函数的最值和正弦定理,属中档题.

| A. | 2 | B. | 3 | C. | 5 | D. | 8 |
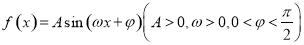 的图象经过三点
的图象经过三点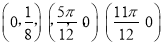 ,且在区间
,且在区间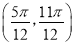 内有唯一的最值,且为最小值.
内有唯一的最值,且为最小值.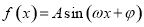 的解析式;
的解析式;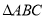 中,
中,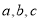 分别是角
分别是角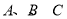 的对边,若
的对边,若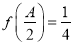 且
且 ,求
,求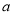 的值.
的值.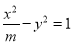 的实轴长是离心率的2倍,则m= .
的实轴长是离心率的2倍,则m= .