题目内容
若点(1,2)在圆(x+a)2+(y+2a)2=5的内部,则实数a的取值范围.
考点:点与圆的位置关系
专题:直线与圆
分析:直接由点P(1,2)在圆(x+a)2+(y+2a)2=5的内部,得到(1+a)2+(2+2a)2<5,求解关于a的一元二次不等式得答案.
解答:
解:∵点P(1,2)在圆(x+a)2+(y+2a)2=5的内部,
∴(1+a)2+(2+2a)2<5.
即a2+2a<0.
解得:-2<a<0.
∴实数a的取值范围为(-2,0).
∴(1+a)2+(2+2a)2<5.
即a2+2a<0.
解得:-2<a<0.
∴实数a的取值范围为(-2,0).
点评:本题考查了点与圆的位置关系,考查了数学转化思想方法,是基础的计算题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
已知a=50.2,b=0.25,c=log0.25,a,b,c的大小关系为( )
| A、b<a<c |
| B、b<c<a |
| C、c<b<a |
| D、c<a<b |
设全集U={1,2,3,4,5,6,7},集合M={2,3,4,5},N={1,4,5,7},则M∩(∁UN)等于( )
| A、{1,7} |
| B、{2,3} |
| C、{2,3,6} |
| D、{1,6,7} |
在三棱锥A-BCD中,M为CD的中点,则
+
(
+
)=( )
| AB |
| 1 |
| 2 |
| BD |
| BC |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
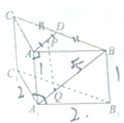 如图,三棱柱ABC-A1B1C1,侧棱AA1⊥平面ABC,A1B1=A1C1=2,AA1=1,∠B1A1C1=120°,D是BC的中点,P是AD的中点,点Q在A1B上且BQ=3QA1
如图,三棱柱ABC-A1B1C1,侧棱AA1⊥平面ABC,A1B1=A1C1=2,AA1=1,∠B1A1C1=120°,D是BC的中点,P是AD的中点,点Q在A1B上且BQ=3QA1