题目内容
下列四个结论中:
(1)如果两个函数都是增函数,那么这两个函数的积运算所得函数为增函数;
(2)奇函数f(x)在[0,+∞)上是增函数,则f(x)在R上为增函数;
(3)既是奇函数又是偶函数的函数只有一个;
(4)若函数f(x)的最小值是a,最大值是b,则f(x)值域为[a,b].
其中正确结论的序号为 .
(1)如果两个函数都是增函数,那么这两个函数的积运算所得函数为增函数;
(2)奇函数f(x)在[0,+∞)上是增函数,则f(x)在R上为增函数;
(3)既是奇函数又是偶函数的函数只有一个;
(4)若函数f(x)的最小值是a,最大值是b,则f(x)值域为[a,b].
其中正确结论的序号为
考点:命题的真假判断与应用
专题:函数的性质及应用
分析:(1)举例说明:当x∈(0,+∞)时,y=x与y=-
均为增函数,y=x•(-
)=-1不是增函数,可判断①;
(2)利用奇函数的性质“奇函数在对称区间上的单调性相同”可判断②;
(3)举例说明,x∈(-1,1)时,f(x)=0与f(x)=
+
均为既是奇函数又是偶函数,可判断③;
(4)构造函数,若a<b,函数f(x)=
,则f(x)值域为{a,b},可判断④.
| 1 |
| x |
| 1 |
| x |
(2)利用奇函数的性质“奇函数在对称区间上的单调性相同”可判断②;
(3)举例说明,x∈(-1,1)时,f(x)=0与f(x)=
| 1-x2 |
| x2-1 |
(4)构造函数,若a<b,函数f(x)=
|
解答:
解:(1),当x∈(0,+∞)时,y=x与y=-
均为增函数,但这两个函数的积运算所得函数为y=x•(-
)=-1不是增函数(为常函数),故(1)错误;
(2)奇函数f(x)在[0,+∞)上是增函数,则f(x)在(-∞,0)上也是增函数,故在R上为增函数,(2)正确;
(3)既是奇函数又是偶函数的函数只有一个,错误.如x∈(-1,1)时,f(x)=0既是奇函数又是偶函数的函数;f(x)=
+
既是奇函数又是偶函数的函数,故(3)错误;
(4)若a<b,函数f(x)=
,即函数f(x)的最小值是a,最大值是b,则f(x)值域为{a,b},而不是[a,b],故(4)错误.
故答案为:(2).
| 1 |
| x |
| 1 |
| x |
(2)奇函数f(x)在[0,+∞)上是增函数,则f(x)在(-∞,0)上也是增函数,故在R上为增函数,(2)正确;
(3)既是奇函数又是偶函数的函数只有一个,错误.如x∈(-1,1)时,f(x)=0既是奇函数又是偶函数的函数;f(x)=
| 1-x2 |
| x2-1 |
(4)若a<b,函数f(x)=
|
故答案为:(2).
点评:本题考查命题的真假判断与应用,着重考查函数的单调性与奇偶性,灵活构造函数是关键,属于中档题.

练习册系列答案
 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案
相关题目
已知M(-c,0),N(c,0),若|PM|-|PN|=c(c>0),则动点P的轨迹是( )
| A、双曲线的左支 |
| B、双曲线的右支 |
| C、以N为端点的射线 |
| D、线段MN |
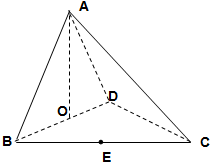 如图,在四面体ABCD中,O、E分别是BD、BC的中点,CA=CB=CD=BD=2,AB=AD=
如图,在四面体ABCD中,O、E分别是BD、BC的中点,CA=CB=CD=BD=2,AB=AD=