已知a∈R.i为虚数单位.若为纯虚数.则a的值为( )A．2B．1C．-2D．-1 题目和参考答案——青夏教育精英家教网—

题目内容

19．已知a∈R，i为虚数单位，若（1-i）（a+i）为纯虚数，则a的值为（　　）

A．

B．

C．

-2

D．

-1

分析直接由复数代数形式的乘法运算化简（1-i）（a+i），再由已知条件列出方程组，求解即可得答案．

解答解：∵（1-i）（a+i）=1+a+（1-a）i为纯虚数，
∴$\left\{\begin{array}{l}{1+a=0}\\{1-a≠0}\end{array}\right.$，解得：a=-1．
故选：D．

点评本题考查了复数代数形式的乘除运算，考查了复数的基本概念，是基础题．

练习册系列答案

天利38套初中名校期末联考测试卷系列答案

10．过点A（1，t）于曲线y=x³-12x相切的直线有3条，则实数t的取值范围为（-12，-11）．

7．已知集合A={x|x²+3x≤0}，集合B={n|n=2k+1，k∈Z}，则A∩B=（　　）

14．设函数f（x）=|x+$\frac{8}{m}$|+|x-2m|（m＞0）．
（Ⅰ）求证：f（x）≥8恒成立；
（Ⅱ）求使得不等式f（1）＞10成立的实数m的取值范围．

4．已知2sinα•tanα=3，且0＜α＜π．
（1）求α的值；
（2）求函数f（x）=4sinxsin（x-α）在$[0，\frac{π}{4}]$上的值域．

11．

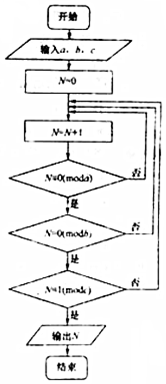若正整数N除以正整m后的余数为n，则记为N=n（modm），例如10=4（mod6）．如图程序框图的算法源于我国古代《孙子算经》中的“孙子定律”的某一环节，执行该框图，输入a=2，b=3，c=5，则输出的N=（　　）

7．已知角α的终边与单位圆交于一点P（-$\frac{4}{5}$，$\frac{3}{5}$），求$\frac{sin（-π-α）tan（-3π+α）}{cos（\frac{11}{2}π-α）sin（\frac{π}{2}+α）}$的值．

8．复数z=1-2i，$\overline{z}$是z的共轭复数，则复平面内复数z•$\overline{z}$-i对应的点所在象限为（　　）

试题分类