题目内容
20.设点P在△ABC内,且$\overrightarrow{AP}$=$\frac{2}{5}$$\overrightarrow{AB}$+$\frac{1}{5}\overrightarrow{AC}$,△ABP的面积为20,则△PBC的面积为40.分析 由$\overrightarrow{AP}=\frac{2}{5}\overrightarrow{AB}+\frac{1}{5}\overrightarrow{AC}$便可得到$\frac{2}{5}(\overrightarrow{PA}+\overrightarrow{PB})=\frac{1}{5}\overrightarrow{CP}$,可取AB中点D,并连接PD,从而可得到$\overrightarrow{CP}=4\overrightarrow{PD}$,这说明C,P,D三点共线,且有$PD=\frac{1}{5}CD$,从而得出S△ABC=100,S△BCD=50,而${S}_{△PBC}=\frac{4}{5}{S}_{△BCD}$,从而便可求出△PBC的面积.
解答 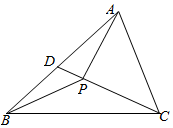 解:$\overrightarrow{AP}=\frac{2}{5}(\overrightarrow{PB}-\overrightarrow{PA})+\frac{1}{5}(\overrightarrow{PC}-\overrightarrow{PA})$;
解:$\overrightarrow{AP}=\frac{2}{5}(\overrightarrow{PB}-\overrightarrow{PA})+\frac{1}{5}(\overrightarrow{PC}-\overrightarrow{PA})$;
∴$\frac{2}{5}(\overrightarrow{PA}+\overrightarrow{PB})=\frac{1}{5}\overrightarrow{CP}$;
如图,取AB中点D,连接PD,则$\overrightarrow{CP}=4\overrightarrow{PD}$;
∴C,P,D三点共线,且$PD=\frac{1}{5}CD$;
∴S△ABC=5S△ABP=100;
∴${S}_{△BCD}=\frac{1}{2}{S}_{△ABC}=50$,${S}_{△PBC}=\frac{4}{5}{S}_{△BCD}=40$.
故答案为:40.
点评 考查向量减法及数乘的几何意义,以及向量的数乘运算,向量加法的平行四边形法则,三角形的面积公式.

| A. | t<2 | B. | t<4 | C. | t>2 | D. | t>4 |
| A. | 直角三角形 | B. | 等腰三角形 | C. | 等边三角形 | D. | 等腰直角三角形 |
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 即不充分也不必要条件 |