题目内容
9.已知a>0,b>0,则“ab>1”是“a+b>2”的( )| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 即不充分也不必要条件 |
分析 根据充分条件和必要条件的定义结合不等式的性质进行判断即可.
解答 解:若a=3,b=$\frac{1}{3}$,满足a+b>2,但ab>1不成立,
∵a2+b2≥2ab,
∴(a+b)2≥4ab,
∵ab>1,
∴(a+b)2>4,
∴a+b>2,
故a>0,b>0,则“ab>1”是“a+b>2”的充分不必要条件,
故选:A
点评 本题主要考查充分条件和必要条件的判断,根据不等式的性质是解决本题的关键.

练习册系列答案
 课堂小作业系列答案
课堂小作业系列答案 黄冈小状元口算速算练习册系列答案
黄冈小状元口算速算练习册系列答案 成功训练计划系列答案
成功训练计划系列答案 倍速训练法直通中考考点系列答案
倍速训练法直通中考考点系列答案 一卷搞定系列答案
一卷搞定系列答案 名校作业本系列答案
名校作业本系列答案
相关题目
14.函数y=ax3+bx2+cx+d的图象如图所示,则( )


| A. | a>0,b>0,c>0 | B. | a>0,b>0,c<0 | C. | a<0,b<0,c>0 | D. | a<0,b<0,c<0 |
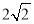 B.
B.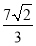 C.
C.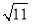 D.
D.
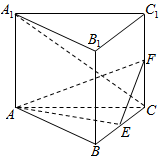 (文科)如图,直三棱柱ABC-A1B1C1的底面是边长为2的正三角形,D,E,F分别是AB,BC,CC1的中点.
(文科)如图,直三棱柱ABC-A1B1C1的底面是边长为2的正三角形,D,E,F分别是AB,BC,CC1的中点.