题目内容
12.若二项式(2x4-$\frac{1}{{x}^{3}}$)n(n∈N+)的展开式中含有x3的项,则n的最小值是6.分析 根据二项式(2x4-$\frac{1}{{x}^{3}}$)n展开式的通项公式,令展开式含x项的指数为3,求出r与n的关系,再求满足条件的最小正整数即可.
解答 解:二项式(2x4-$\frac{1}{{x}^{3}}$)n(n∈N+)展开式的通项公式为:
Tr+1=Cnr•(2x4)n-r•${(-\frac{1}{{x}^{3}})}^{r}$=(-1)r•2n-r•Cnr•x4n-7r;
令4n-7r=3,
即7r=4n-3,
解得r=$\frac{4n-3}{7}$,
所以4n-3是7的倍数;
所以满足条件的最小正整数是6.
故答案为:6.
点评 本题主要考查二项式定理的应用问题.解题的关键是利用展开式中x的指数等于3,求出r和n的关系.是基础题目.

练习册系列答案
相关题目
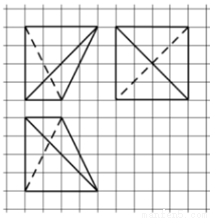
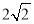 B.
B.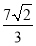 C.
C.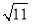 D.
D.