题目内容
8.已知正n棱锥的体积V为定值,试确定其侧面与底面所成的二面角的大小,使得正n棱锥的表面积取得最小值.分析 设其侧面与底面所成的二面角的大小为α,以正四棱锥为例,设正四棱锥的底面正方形的边长为2a,高为h,建立关系,利用基本不等式求解表面积最小时的体积与边长的关系,从而确定其侧面与底面所成的二面角的大小.
解答 解:设其侧面与底面所成的二面角的大小为α,以正四棱锥为例,体积V为定值,设正四棱锥的底面正方形的边长为2a,高为h,
则侧面的高为h′=$\sqrt{{h}^{2}+{a}^{2}}$,
棱锥的体积V=$\frac{1}{3}$Sh=$\frac{1}{3}$4a2h,则${a}^{2}=\frac{3v}{4h}$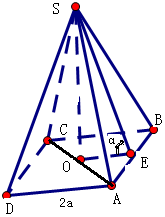 表面积S=4×$\frac{1}{2}$×h′×2a=4a×h′=4a$\sqrt{{h}^{2}+{a}^{2}}$=4×$\sqrt{\frac{3V}{4h}×({h}^{2}-\frac{3V}{4h})}$=4×$\sqrt{\frac{3Vh}{4}+\frac{9{V}^{2}}{16{h}^{2}}}$
表面积S=4×$\frac{1}{2}$×h′×2a=4a×h′=4a$\sqrt{{h}^{2}+{a}^{2}}$=4×$\sqrt{\frac{3V}{4h}×({h}^{2}-\frac{3V}{4h})}$=4×$\sqrt{\frac{3Vh}{4}+\frac{9{V}^{2}}{16{h}^{2}}}$
∵$\frac{3Vh}{8}+\frac{3Vh}{8}+\frac{9{V}^{2}}{16{h}^{2}}$≥3×$\root{3}{\frac{3V×3V×9{V}^{2}}{64×16}}$=$\frac{9V}{4}\root{3}{\frac{3V}{16}}$,
(当且仅当$\frac{3Vh}{8}=\frac{9{V}^{2}}{16{h}^{2}}$时,即h=$\root{3}{\frac{3V}{2}}$取等号).
而此时侧面与底面所成的二面角α,有$tanα=\frac{h}{a}$,
可得:$tanα=\frac{4(\frac{3}{2}V)^{\frac{2}{3}}}{3V}$
故得:侧面与底面所成的二面角α=arctan($\frac{4(\frac{3}{2}V)^{\frac{2}{3}}}{3V}$).
点评 本题考察了正n棱锥的体积V与底面积,表面积之间的关系,基本不等式求解表面积最小时的体积与边长的关系,从而确定其侧面与底面所成的二面角的大小是解题的关键.属于中档题.

| A. | f(b)<f(a)<f(c) | B. | f(c)<f(b)<f(a) | C. | f(c)<f(a)<f(b) | D. | f(b)<f(c)<f(a) |