题目内容
下列几个命题，正确的有 ．（填正确命题的序号）
①若方程x2+（a-3）x+a=0有一个正实根，一个负实根，则a＜0；
②若函数y=f（x+1）为偶函数，则函数y=f（x）的图象关于直线x=-1成轴对称；
③函数f（x）=log
（6-x-x2）的单调递增区间是[-
，2）．
①若方程x2+（a-3）x+a=0有一个正实根，一个负实根，则a＜0；
②若函数y=f（x+1）为偶函数，则函数y=f（x）的图象关于直线x=-1成轴对称；
③函数f（x）=log
| 1 |
| 3 |
| 1 |
| 2 |
考点：命题的真假判断与应用
专题：简易逻辑
分析：对于①，结合函数f（x）=x2+（a-3）x+a的图象可知，只需x=0时，函数的图象在x轴下方即可，据此列出不等式；
对于②，根据偶函数的性质以及图象变换的方法求解；
对于③，先求函数的定义域，然后结合复合函数的单调性求法，将问题转化为内函数y=6-x-x2的单调区间求法．
对于②，根据偶函数的性质以及图象变换的方法求解；
对于③，先求函数的定义域，然后结合复合函数的单调性求法，将问题转化为内函数y=6-x-x2的单调区间求法．
解答：
解：对于①，令f（x）=x2+（a-3）x+a，要使x2+（a-3）x+a=0有一个正实根，一个负实根，只需f（0）＜0，即a＜0即可，故①正确；
对于②，因为函数y=f（x+1）为偶函数，所以图象关于y轴对称，又函数y=f（x）图象可由y=f（x+1）图象沿x轴向右平移一个单位得到，所以y=f（x）图象关于直线x=1对称，故②错误；
对于③，易知函数的定义域为（-3，2），令t=6-x-x2，则y=log
t，外函数为减函数，所以要求原函数的增区间，即求函数t=6-x-x2在（-3，2）上的减区间，即[-
，2)，故③正确．
故答案为①③．
对于②，因为函数y=f（x+1）为偶函数，所以图象关于y轴对称，又函数y=f（x）图象可由y=f（x+1）图象沿x轴向右平移一个单位得到，所以y=f（x）图象关于直线x=1对称，故②错误；
对于③，易知函数的定义域为（-3，2），令t=6-x-x2，则y=log
| 1 |
| 3 |
| 1 |
| 2 |
故答案为①③．
点评：本题以命题真假的判断为载体，考查了方程根的分布、函数的奇偶性及图象平移以及复合函数的单调区间求法等知识，属于基础题，难度不大．
练习册系列答案
阅读快车系列答案
相关题目
下列说法正确的是（ ）
| A、命题“若p或q”为真命题，则p，q中至少有一个为真命题 |
| B、命题“?x0∈R，x02+x0-1＜0”的否定是“?x∈R，x2+x-1＞0” |
| C、命题“若x=y，则sinx=siny”的逆否命题为假命题 |
| D、命题“若x2=1，则x=1”的否命题为“若x2=1，则x≠1” |
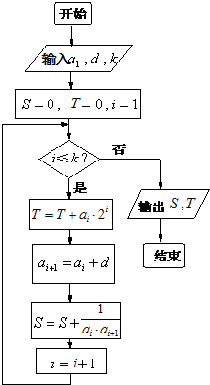如图所示，程序框图给出了无穷正项数列{an}满足的条件，且当k=5时，输出的S是
设y=f（x）为定义在R上的偶函数，当x≤-1时，y=f（x）的图象是经过点（-2，2），斜率为-1的一条射线，又当x∈[-1，0]时，y=f（x）的图象是顶点在（0，2），且过点（-1，1）的一段抛物线．