题目内容
已知点A(3,0),F(2,0),在双曲线x2-
=1上求一点P,使|PA|+
|PF|的值最小.
| y2 |
| 3 |
| 1 |
| 2 |
考点:双曲线的简单性质
专题:计算题,圆锥曲线的定义、性质与方程,圆锥曲线中的最值与范围问题
分析:根据题意,算出双曲线的离心率e=2,右准线为l:x=
.作AN⊥l于N,交双曲线右支于P,连结FP,根据圆锥曲线统一定义得到|PA|+
|PF|=|PA|+|PN|.由平几知识可得:当A、P、N三点共线时,|PA|+|PN|=|AN|达到最小值,由此即可求出点P的坐标和|PA|+
|PF|的最小值.
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
解答:
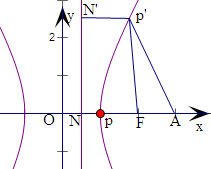 解∵双曲线方程为x2-
解∵双曲线方程为x2-
=1,
∴a=1,b=
,c=2,
可得离心率e=
=2,
=
,所以右准线为l:x=
,
作AN⊥l于N,交双曲线右支于P,连结FP,则
由圆锥曲线统一定义得
=e,可得|PF|=e|PN|=2|PN|,
∴|PN|=
|PF|,因此,|PA|+
|PF|=|PA|+|PN|,
当且仅当A、P、N三点共线时,|PA|+|PN|=|AN|达到最小值.
此时,在x2-
=1中令y=0,得x=±1,
∵x>0,∴取x=1
即当P的坐标为(1,0)时,|PA|+
|PF|的最小值为|AN|=3-
=
.
 解∵双曲线方程为x2-
解∵双曲线方程为x2-| y2 |
| 3 |
∴a=1,b=
| 3 |
可得离心率e=
| c |
| a |
| a2 |
| c |
| 1 |
| 2 |
| 1 |
| 2 |
作AN⊥l于N,交双曲线右支于P,连结FP,则
由圆锥曲线统一定义得
| |PF| |
| |PN| |
∴|PN|=
| 1 |
| 2 |
| 1 |
| 2 |
当且仅当A、P、N三点共线时,|PA|+|PN|=|AN|达到最小值.
此时,在x2-
| y2 |
| 3 |
∵x>0,∴取x=1
即当P的坐标为(1,0)时,|PA|+
| 1 |
| 2 |
| 1 |
| 2 |
| 5 |
| 2 |
点评:本题着重考查了双曲线的标准方程与简单几何性质、圆锥曲线的统一定义等知识,属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目