题目内容
3.${∫}_{0}^{1}$(-$\sqrt{1-{x}^{2}}$)dx=-$\frac{π}{4}$.分析 根据定积分的几何意义即可求出
解答 解:${∫}_{0}^{1}$(-$\sqrt{1-{x}^{2}}$)dx=-${∫}_{0}^{1}$$\sqrt{1-{x}^{2}}$dx,
因为${∫}_{0}^{1}$$\sqrt{1-{x}^{2}}$dx表示以原点为圆心以1为半径的圆的面积的四分之一,
所以${∫}_{0}^{1}$$\sqrt{1-{x}^{2}}$dx=$\frac{π}{4}$,
故:${∫}_{0}^{1}$(-$\sqrt{1-{x}^{2}}$)dx=-${∫}_{0}^{1}$$\sqrt{1-{x}^{2}}$dx=-$\frac{π}{4}$,
故答案为:-$\frac{π}{4}$
点评 本题考查了定积分几何意义,属于基础题

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
13.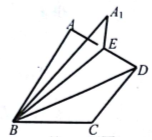 如图,在直二面角A-BD-C中,△ABD、△CBD均是以BD为斜边的等腰直角三角形,取AD中点E,将△ABE沿BE翻折到△A1BE,在△ABE的翻折过程中,下列不可能成立的是( )
如图,在直二面角A-BD-C中,△ABD、△CBD均是以BD为斜边的等腰直角三角形,取AD中点E,将△ABE沿BE翻折到△A1BE,在△ABE的翻折过程中,下列不可能成立的是( )
 如图,在直二面角A-BD-C中,△ABD、△CBD均是以BD为斜边的等腰直角三角形,取AD中点E,将△ABE沿BE翻折到△A1BE,在△ABE的翻折过程中,下列不可能成立的是( )
如图,在直二面角A-BD-C中,△ABD、△CBD均是以BD为斜边的等腰直角三角形,取AD中点E,将△ABE沿BE翻折到△A1BE,在△ABE的翻折过程中,下列不可能成立的是( )| A. | BC与平面A1BE内某直线平行 | B. | CD∥平面A1BE | ||
| C. | BC与平面A1BE内某直线垂直 | D. | BC⊥A1B |
11.若实数x,y满足约束条件$\left\{\begin{array}{l}x-2y+3≥0\\ y≥x\\ x≥1\end{array}\right.$,则$z=\frac{y}{x+1}$的最小值为( )
| A. | $\sqrt{3}$ | B. | 1 | C. | $\frac{3}{4}$ | D. | $\frac{1}{2}$ |
12.已知sin($\frac{π}{5}$-α)=$\frac{1}{4}$,则cos(2α+$\frac{3π}{5}$)=( )
| A. | -$\frac{7}{8}$ | B. | $\frac{7}{8}$ | C. | $\frac{1}{8}$ | D. | -$\frac{1}{8}$ |