题目内容
15．在?ABCD中，点E满足$\overrightarrow{CE}$=$\overrightarrow{ED}$，若$\overrightarrow{EB}$=m$\overrightarrow{AB}$+n$\overrightarrow{AD}$，则m-n等于（ ）| A． | $\frac{3}{2}$ | B． | $\frac{2}{3}$ | C． | -$\frac{2}{3}$ | D． | $\frac{5}{3}$ |
分析 解：可得E为DC中点，则$\overrightarrow{EB}=\overrightarrow{EC}+\overrightarrow{CB}$=$\frac{1}{2}\overrightarrow{AB}$-$\overrightarrow{AD}$，即m-n=$\frac{3}{2}$．
解答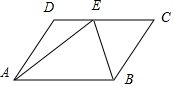 
解：∵点E满足$\overrightarrow{CE}$=$\overrightarrow{ED}$，∴E为DC中点，
则$\overrightarrow{EB}=\overrightarrow{EC}+\overrightarrow{CB}$=$\frac{1}{2}\overrightarrow{AB}$-$\overrightarrow{AD}$，
∴$m=\frac{1}{2}$，n=-1，即m-n=$\frac{3}{2}$，
故选：A．
点评 本题考查了向量的线性运算，属于中档题．
练习册系列答案
阅读快车系列答案
相关题目
6．随机变量ξ服从二项分布ξ～B（n，P），且E（ξ）=300，D（ξ）=200，则$\frac{n}{p}$等于（ ）
| A． | 3200 | B． | 2700 | C． | 1350 | D． | 1200 |
20．圆锥的侧面展开图是圆心角为α，半径为$\sqrt{3}$的扇形，当圆锥的体积最大时，α的值为（ ）
| A． | $\frac{\sqrt{3}π}{3}$ | B． | $\frac{2\sqrt{3}π}{3}$ | C． | $\frac{\sqrt{6}π}{3}$ | D． | $\frac{2\sqrt{6}π}{3}$ |
7．现有4道数学试题，老师安排甲、乙、丙三位同学解答，要求每人至少解答一道，则不同的安排方法有（ ）
| A． | 18种 | B． | 24种 | C． | 36种 | D． | 42种 |