题目内容
19.设函数$f(x)=sin2x+\sqrt{3}cos2x$(1)求函数f(x)的最小正周期;
(2)当x∈[0,$\frac{π}{6}$]时,求函数f(x)的最大值和最小值.
分析 (1)使用辅助角公式化简f(x)=2sin(2x+$\frac{π}{3}$),代入周期公式得到f(x)的周期;
(2)根据x的范围求得2x+$\frac{π}{3}$的范围,结合正弦函数的性质得出f(x)的最值.
解答 解:(1)f(x)=sin2x+$\sqrt{3}$cos2x=2sin(2x+$\frac{π}{3}$),∴f(x)的最小正周期T=$\frac{2π}{2}$=π.
(2)∵x∈[0,$\frac{π}{6}$],∴2x+$\frac{π}{3}$∈[$\frac{π}{3}$,$\frac{2π}{3}$],∴当2x+$\frac{π}{3}$=$\frac{π}{2}$时,f(x)取得最大值2,2x+$\frac{π}{3}$=$\frac{π}{3}$时,f(x)取得最小值$\sqrt{3}$.
点评 本题考查了三角函数的恒等变换,正弦函数的图象性质,属于基础题.

练习册系列答案
相关题目
14.$\left\{{\overrightarrow a,\overrightarrow b,\overrightarrow c}\right\}$是空间的一个单位正交基底,$\overrightarrow p$在基底$\left\{{\overrightarrow a,\overrightarrow b,\overrightarrow c}\right\}$下的坐标为(2,1,5),则$\overrightarrow p$在基底$\left\{{\overrightarrow a+\overrightarrow b,\overrightarrow b+\overrightarrow c,\overrightarrow a+\overrightarrow c}\right\}$下的坐标为( )
| A. | (-1,2,3) | B. | (1,-2,3) | C. | (1,2,-3) | D. | (-3,2,1) |
4.如图,网格纸的各小格都是正方形,粗实线画出的是一个凸多面体的三视图(两个矩形,一个直角三角形),则这个几何体可能为( )
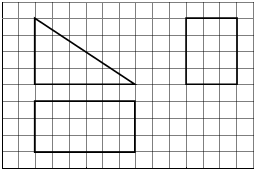

| A. | 三棱台 | B. | 三棱柱 | C. | 四棱柱 | D. | 四棱锥 |
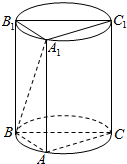 如图,四边形BCC1B1是圆柱的轴截面.AA1是圆柱的一条母线,已知AB=4,AC=2$\sqrt{2}$,AA1=3.
如图,四边形BCC1B1是圆柱的轴截面.AA1是圆柱的一条母线,已知AB=4,AC=2$\sqrt{2}$,AA1=3.