题目内容
设f(x)是连续的偶函数,且当x>0时是单调函数,则满足 的所有x之和为
的所有x之和为
- A.
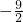
- B.

- C.-8
- D.8
C
分析:f(x)为偶函数推出f(-x)=f(x),x>0时f(x)是单调函数,推出f(x)不是周期函数.所以若f(a)=f(b)?a=b或a=-b,再利用根与系数的关系进行求解;
解答:∵f(x)为偶函数,
∴(2x)=f(-2x)
∵当x>0时f(x)是单调函数,
又满足 ,
,
∴2x= 或-2x=
或-2x= ,
,
可得,2x2+7x-1=0或2x2+9x+1=0,两个方程都有解.
∴x1+x2= 或x3+x4=
或x3+x4=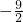 ,
,
∴x1+x2+x3+x4= ,
,
故选C.
点评:本题主要函数奇偶性和单调性的性质,考查了函数的单调性和奇偶性与方程根的联系,属于函数性质的综合应用.
分析:f(x)为偶函数推出f(-x)=f(x),x>0时f(x)是单调函数,推出f(x)不是周期函数.所以若f(a)=f(b)?a=b或a=-b,再利用根与系数的关系进行求解;
解答:∵f(x)为偶函数,
∴(2x)=f(-2x)
∵当x>0时f(x)是单调函数,
又满足
 ,
,∴2x=
 或-2x=
或-2x= ,
,可得,2x2+7x-1=0或2x2+9x+1=0,两个方程都有解.
∴x1+x2=
 或x3+x4=
或x3+x4=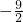 ,
,∴x1+x2+x3+x4=
 ,
,故选C.
点评:本题主要函数奇偶性和单调性的性质,考查了函数的单调性和奇偶性与方程根的联系,属于函数性质的综合应用.

练习册系列答案
相关题目
设f(x)是连续的偶函数,且当x>0时f(x)是单调函数,则满足f(x)=f(
)的所有x之和为( )
| x+3 |
| x+4 |
| A、-3 | B、3 | C、-8 | D、8 |