题目内容
已知三个函数f(x)=2x+x,g(x)=x-2,h(x)=log2x+x的零点依次为a,b,c,则a,b,c的大小关系是 .
考点:函数零点的判定定理
专题:函数的性质及应用
分析:根据函数解析式判断出f(x)=2x+x,g(x)=x-2,h(x)=log2x+x都是单调递增函数,运用函数零点定理判断a,b,c的范围即可得a,b,c的大小.
解答:
解:由于f(-1)=
-1=-
<0,f(0)=1>0,
故f(x)=2x+x的零点a∈(-1,0).
∵g(2)=0∴g(x)的零点b=2;
∵h(
)=-1+
=-
<0,h(1)=1>0
∴h(x)的零点c∈(
,1),
由于函数f(x)=2x+x,g(x)=x-2,h(x)=log2x+x均是定义域上的单调增函数,
∴a<c<b.
故答案为:a<c<b.
| 1 |
| 2 |
| 1 |
| 2 |
故f(x)=2x+x的零点a∈(-1,0).
∵g(2)=0∴g(x)的零点b=2;
∵h(
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∴h(x)的零点c∈(
| 1 |
| 2 |
由于函数f(x)=2x+x,g(x)=x-2,h(x)=log2x+x均是定义域上的单调增函数,
∴a<c<b.
故答案为:a<c<b.
点评:本题考查了函数的单调性,在求解函数零点的范围问题中的应用,结合函数零点定理判断即可.

练习册系列答案
 寒假大串联黄山书社系列答案
寒假大串联黄山书社系列答案
相关题目
若函数y=ax-x-a有两个零点,则a的取值范围是( )
| A、(1,+∞) | B、(0,1) |
| C、(0,+∞) | D、∅ |
设P是?ABCD对角线的交点,O为空间任意一点(不在平面ABCD上),则
+
+
+
等于( )
| OA |
| OB |
| OC |
| OD |
A、4
| ||
B、6
| ||
C、2
| ||
D、
|
 中,若
中,若 ,则
,则 的值是( )
的值是( ) B.
B. C.
C. D.
D.
 的左、右焦点分别为
的左、右焦点分别为 ,以
,以 为圆心,
为圆心, (
( 为椭圆中心)为半径作圆
为椭圆中心)为半径作圆 ,且
,且 恰好为圆
恰好为圆 B.
B. C.
C. D.
D.
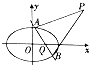 已知椭圆C:
已知椭圆C: