题目内容
若函数y=ax-x-a有两个零点，则a的取值范围是（ ）
| A、（1，+∞） | B、（0，1） |
| C、（0，+∞） | D、∅ |
考点：函数零点的判定定理
专题：计算题,函数的性质及应用,导数的综合应用
分析：分当0＜a＜1时及当a＞1时讨论，结合函数的单调性及取值范围，运用函数零点的判定定理确定个数即可．
解答：
解：①当0＜a＜1时，
易知函数y=ax-x-a是减函数，
故最多有一个零点，故不成立；
②当a＞1时，y′=lna•ax-1，
故当ax＜
时，y′＜0；
当ax＞
时，y′＞0；
故y=ax-x-a在R上先减后增，
且当x→-∞时，y→+∞，当x→+∞时，y→+∞，
且当x=0时，y=1-0-a＜0；
故函数y=ax-x-a有两个零点；
故成立；
故选A．
易知函数y=ax-x-a是减函数，
故最多有一个零点，故不成立；
②当a＞1时，y′=lna•ax-1，
故当ax＜
| 1 |
| lna |
当ax＞
| 1 |
| lna |
故y=ax-x-a在R上先减后增，
且当x→-∞时，y→+∞，当x→+∞时，y→+∞，
且当x=0时，y=1-0-a＜0；
故函数y=ax-x-a有两个零点；
故成立；
故选A．
点评：本题综合考查了导数的综合应用及函数零点判定定理的应用，同时考查了分类讨论的思想应用，属于基础题．
练习册系列答案
习题精选系列答案
相关题目
的图象；
的离心率为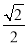
，且过点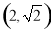
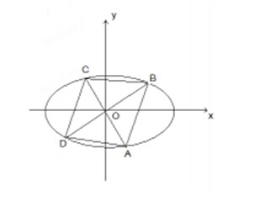（2）四边形ABCD的顶点在椭圆上，且对角线AC，BD过原点O，若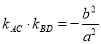
的最值：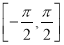
上随机取一个
，
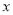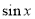的值介于
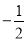与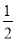
之间的概率为（ ）
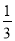（B）
（C）
（D）
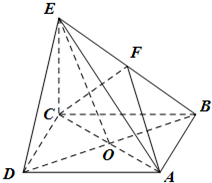在四棱锥E-ABCD中，底面ABCD是正方形，AC与BD交于点O，EC⊥平面ABCD，F为BE的中点．
如图，正方体ABCD-A1B1C1D1中，E、F分别是CD、CC1的中点．证明：EF∥平面AB1D1．
如图，在三棱锥P-ABC中，AB=5，BC=4，AC=3，点D是线段PB的中点，平面PAC⊥平面ABC．