题目内容
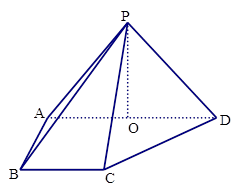
(本题满分13分)如图,在四棱锥P-ABCD中,侧面PAD⊥底面ABCD,侧棱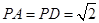 ,
,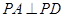 ,底面
,底面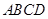 为直角梯形,其中BC∥AD, AB⊥AD,
为直角梯形,其中BC∥AD, AB⊥AD, 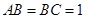 ,O为AD中点.
,O为AD中点.
(1)求直线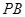 与平面
与平面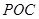 所成角的余弦值;
所成角的余弦值;
(2)求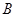 点到平面
点到平面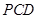 的距离
的距离
(3)线段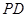 上是否存在点
上是否存在点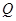 ,使得二面角
,使得二面角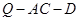 的余弦值为
的余弦值为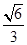 ?若存在,求出
?若存在,求出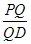 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
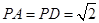 ,
,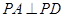 ,底面
,底面 为直角梯形,其中BC∥AD, AB⊥AD,
为直角梯形,其中BC∥AD, AB⊥AD, 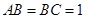 ,O为AD中点.
,O为AD中点.
(1)求直线
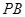 与平面
与平面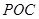 所成角的余弦值;
所成角的余弦值;(2)求
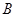 点到平面
点到平面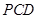 的距离
的距离(3)线段
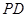 上是否存在点
上是否存在点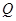 ,使得二面角
,使得二面角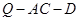 的余弦值为
的余弦值为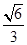 ?若存在,求出
?若存在,求出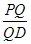 的值;若不存在,请说明理由.
的值;若不存在,请说明理由. (1) 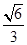 ;(2)
;(2) ;(3)存在,且
;(3)存在,且 。
。
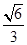 ;(2)
;(2) ;(3)存在,且
;(3)存在,且 。
。本试题主要是考查了立体几何中线面角的求解,二面角的问题,以及点到面的距离。
(1)先确定出平面的垂线,然后利用已知的关系式来得到线面角的表示,进而求解。
(2)利用等体积法得到点到面的距离。
(3)建立空间直角坐标系,进而表示平面的法向量,利用向量与向量的夹角,得到二面角的平面角。
解:(1) 在△PAD中PA=PD, O为AD中点,所以PO⊥AD,
又侧面PAD⊥底面ABCD, 平面 平面ABCD=AD,
平面ABCD=AD,  平面PAD,
平面PAD,
所以PO⊥平面ABCD.
又在直角梯形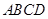 中,易得
中,易得 ;所以以
;所以以 为坐标原点,
为坐标原点, 为
为 轴,
轴, 为
为
轴, 为
为 轴建立空间直角坐标系.
轴建立空间直角坐标系.
则 ,
, ,
,
 ,
, ;
;

 ,易证:
,易证: ,所以
,所以 平面
平面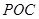 的法向量,
的法向量,

所以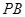 与平面
与平面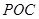 所成角的余弦值为
所成角的余弦值为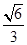 ; ……………………………….4分
; ……………………………….4分
(2) ,设平面PDC的法向量为
,设平面PDC的法向量为 ,
,
则 ,取
,取 得
得
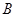 点到平面
点到平面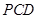 的距离
的距离 ……………….8分
……………….8分
(3)假设存在,则设
 ,
,
因为 ,
, ,
,
所以 ,
,
设平面 的法向量为
的法向量为 ,则
,则
取 ,得
,得
平面 的有一个法向量为
的有一个法向量为
因为二面角 的余弦值为
的余弦值为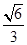 ,所以
,所以
得到 得
得 或
或 (舍)
(舍)
所以存在,且 ………………… 13分
………………… 13分
(1)先确定出平面的垂线,然后利用已知的关系式来得到线面角的表示,进而求解。
(2)利用等体积法得到点到面的距离。
(3)建立空间直角坐标系,进而表示平面的法向量,利用向量与向量的夹角,得到二面角的平面角。
解:(1) 在△PAD中PA=PD, O为AD中点,所以PO⊥AD,
又侧面PAD⊥底面ABCD, 平面
 平面ABCD=AD,
平面ABCD=AD,  平面PAD,
平面PAD,所以PO⊥平面ABCD.
又在直角梯形
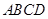 中,易得
中,易得 ;所以以
;所以以 为坐标原点,
为坐标原点, 为
为 轴,
轴, 为
为
轴,
 为
为 轴建立空间直角坐标系.
轴建立空间直角坐标系.则
 ,
, ,
,
 ,
, ;
;
 ,易证:
,易证: ,所以
,所以 平面
平面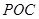 的法向量,
的法向量, 
所以
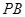 与平面
与平面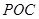 所成角的余弦值为
所成角的余弦值为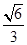 ; ……………………………….4分
; ……………………………….4分(2)
 ,设平面PDC的法向量为
,设平面PDC的法向量为 ,
,则
 ,取
,取 得
得
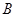 点到平面
点到平面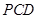 的距离
的距离 ……………….8分
……………….8分(3)假设存在,则设

 ,
,因为
 ,
, ,
,
所以
 ,
,设平面
 的法向量为
的法向量为 ,则
,则
取
 ,得
,得
平面
 的有一个法向量为
的有一个法向量为
因为二面角
 的余弦值为
的余弦值为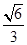 ,所以
,所以
得到
 得
得 或
或 (舍)
(舍)所以存在,且
 ………………… 13分
………………… 13分
练习册系列答案
相关题目
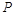 、
、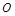 分别是正四棱柱
分别是正四棱柱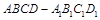 上、下底面的中
上、下底面的中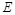 是
是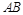 的中点,
的中点,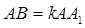 .
.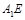 ∥平面
∥平面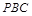 ;
;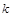 取何值时,
取何值时,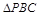 的重心?
的重心? 
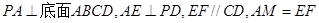
 ,求直线AC与平面EAM所成角的正弦值
,求直线AC与平面EAM所成角的正弦值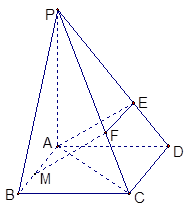











 ),可得这个几何体的体积是( )
),可得这个几何体的体积是( )













