题目内容
已知|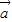 |=|
|=|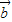 |=2,(
|=2,(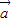 +2
+2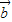 )•(
)•(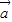 -
-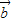 )=-2,则
)=-2,则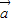 与
与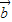 的夹角为 .
的夹角为 .
【答案】分析:由已知中|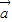 |=|
|=|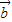 |=2,(
|=2,(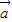 +2
+2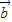 )•(
)•(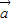 -
-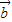 )=-2,可求出cosθ=
)=-2,可求出cosθ= ,进而根据向量夹角的范围为0≤θ≤π,得到答案.
,进而根据向量夹角的范围为0≤θ≤π,得到答案.
解答:解:∵|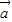 |=|
|=|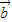 |=2,
|=2,
∴|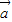 |2=|
|2=|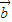 |2=4
|2=4
∵(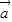 +2
+2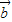 )•(
)•(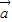 -
-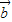 )=-2
)=-2
展开得:|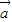 |2+
|2+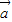 •
•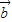 -2|
-2|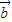 |2=4cosθ-4=-2,
|2=4cosθ-4=-2,
即cosθ=
又∵0≤θ≤π
故θ=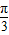
故答案为: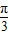
点评:本题考查的知识点是数量积表示两个向量的夹角,其中根据已知计算出cosθ= ,是解答的关键.
,是解答的关键.
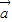 |=|
|=|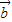 |=2,(
|=2,(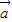 +2
+2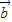 )•(
)•(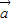 -
-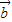 )=-2,可求出cosθ=
)=-2,可求出cosθ= ,进而根据向量夹角的范围为0≤θ≤π,得到答案.
,进而根据向量夹角的范围为0≤θ≤π,得到答案.解答:解:∵|
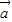 |=|
|=|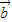 |=2,
|=2,∴|
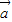 |2=|
|2=|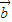 |2=4
|2=4∵(
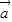 +2
+2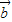 )•(
)•(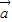 -
-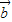 )=-2
)=-2展开得:|
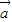 |2+
|2+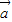 •
•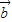 -2|
-2|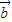 |2=4cosθ-4=-2,
|2=4cosθ-4=-2,即cosθ=

又∵0≤θ≤π
故θ=
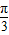
故答案为:
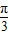
点评:本题考查的知识点是数量积表示两个向量的夹角,其中根据已知计算出cosθ=
 ,是解答的关键.
,是解答的关键. 
练习册系列答案
相关题目
已知α∈(
,π),cosα=-
,则tan(α-
)等于( )
| π |
| 2 |
| 4 |
| 5 |
| π |
| 4 |
A、
| ||
| B、7 | ||
C、-
| ||
| D、-7 |
已知-
<x<0,sinx+cosx=
,则
等于( )
| π |
| 2 |
| 1 |
| 5 |
| sinx-cosx |
| sinx+cosx |
| A、-7 | ||
B、-
| ||
| C、7 | ||
D、
|