题目内容
11.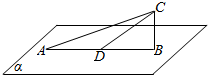 如图,平面α⊥平面ABC,D为线段AB的中点,|AB|=2$\sqrt{3}$,∠CDB=30°,P为面α内的动点,且P到直线CD的距离为1,则∠APB的最大值为 )
如图,平面α⊥平面ABC,D为线段AB的中点,|AB|=2$\sqrt{3}$,∠CDB=30°,P为面α内的动点,且P到直线CD的距离为1,则∠APB的最大值为 )| A. | 60° | B. | 90° | C. | 120° | D. | 150° |
分析 由题意推出到直线的距离为1的P的轨迹是圆柱,得到平面α的图形是椭圆,然后∠APB的最大值即可.
解答  解:空间中到直线CD的距离为1的点构成一个圆柱面,它和面α相交得一椭圆,所以P在α内的轨迹为一个椭圆,D为椭圆的中心,b=1,a=$\frac{1}{sin60°}$=$\frac{2}{\sqrt{3}}$,则c=$\frac{1}{\sqrt{3}}$,
解:空间中到直线CD的距离为1的点构成一个圆柱面,它和面α相交得一椭圆,所以P在α内的轨迹为一个椭圆,D为椭圆的中心,b=1,a=$\frac{1}{sin60°}$=$\frac{2}{\sqrt{3}}$,则c=$\frac{1}{\sqrt{3}}$,
于是A,B为椭圆的焦点,椭圆上点关于两焦点的张角在短轴的端点取得最大,
故为120°.
故选:C.
点评 本题是立体几何与解析几何知识交汇试题,题目新,考查空间想象能力,计算能力.

练习册系列答案
 智慧小复习系列答案
智慧小复习系列答案
相关题目
19.下列函数是偶函数的是( )
| A. | $y=\frac{1}{x}+x$ | B. | y=x3 | C. | $y=\sqrt{x}$ | D. | y=x2+1 |
6.在棱长为a正方体ABCD-A1B1C1D1中,AC1和BD1相交于点O,则有( )
| A. | $\overrightarrow{AB}•\overrightarrow{{A_1}C}=2{a^2}$ | B. | $\overrightarrow{AB}•\overrightarrow{AC}=\sqrt{2}{a^2}$ | C. | $\overrightarrow{AB}•\overrightarrow{{A_1}O}=\frac{1}{2}{a^2}$ | D. | $\overrightarrow{BC}•\overrightarrow{AO}={a^2}$ |
3.已知数列{an}{n=1,2,3…,2015},圆C1:x2+y2-4x-4y=0,圆C2:x2+y2-2anx-2a2006-ny=0,若圆C2平分圆C1的周长,则{an}的所有项的和为( )
| A. | 2014 | B. | 2015 | C. | 4028 | D. | 4030 |
1.若${∫}_{0}^{1}$(x2+mx)dx=$\frac{4}{3}$,则在(x2-3x+m)5的展开式中,含x项的系数为( )
| A. | -240 | B. | -120 | C. | 0 | D. | 120 |
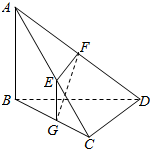 如图,在三棱锥A-BCD中,AB⊥平面BCD,BC⊥CD,E,F,G分别是AC,AD,BC的中点.求证:
如图,在三棱锥A-BCD中,AB⊥平面BCD,BC⊥CD,E,F,G分别是AC,AD,BC的中点.求证: