题目内容
20.设点P(x,y)是曲线a|x|+b|y|=1(a≥0,b≥0)上任意一点,其坐标(x,y)均满足$\frac{x^2}{2}+{y^2}≤1$,则$\sqrt{2}$a+b取值范围为[2,+∞).分析 画出椭圆的区域,曲线表示的形状,利用图形推出a,b的范围,然后推出结果.
解答 解:满足$\frac{x^2}{2}+{y^2}≤1$,是以F1(-1,0),F2(1,0)为焦点的椭圆内部,
曲线a|x|+b|y|=1(a>0,b>0)为如下图所示的菱形ABCD,$C(\frac{1}{a},0),D(0,\frac{1}{b})$.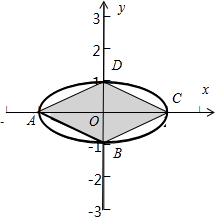
$\sqrt{{x}^{2}+{y}^{2}+2y+1}+\sqrt{{x}^{2}+{y}^{2}-2y+1}≤2\sqrt{2}$,所以$\frac{1}{a}≤\sqrt{2},\frac{1}{b}≤1$,
即$a≥\frac{{\sqrt{2}}}{2},b≥1$.
所以$\sqrt{2}a+b≥\sqrt{2}×\frac{{\sqrt{2}}}{2}+1=2$.
则$\sqrt{2}$a+b取值范围为:[2,+∞).
故答案为:[2,+∞).
点评 本题考查椭圆的简单性质以及不等式的简单性质的应用,考查计算能力.

练习册系列答案
 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案
相关题目
8.我国古代数学名著《九章算术》有“米谷粒分”题:粮仓开仓收粮,有人送来米1534石,验得米内夹谷,抽样取米一把,数得254粒肉夹谷56粒,则这批米内夹谷约为( )
| A. | 1365石 | B. | 338 石 | C. | 168石 | D. | 134石 |
6.在区间[1,5]和[2,4]上分别各取一个数,记为m和n,则方程$\frac{x^2}{m^2}+\frac{y^2}{n^2}=1$表示焦点在x轴上的椭圆的概率是( )
| A. | $\frac{1}{3}$ | B. | $\frac{1}{2}$ | C. | $\frac{2}{3}$ | D. | $\frac{3}{4}$ |
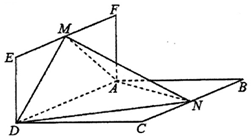 如图,平面ABCD⊥平面ADEF,四边形ABCD为菱形,四边形ADEF为矩形,M,N分别是EF,BC的中点,AB=2AF,∠CBA=
如图,平面ABCD⊥平面ADEF,四边形ABCD为菱形,四边形ADEF为矩形,M,N分别是EF,BC的中点,AB=2AF,∠CBA=