Question

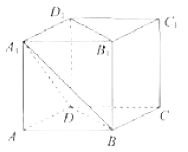
【题目】如图，在四棱锥中，PA⊥平面ABCD，CD⊥AD，BC∥AD，.

（Ⅰ）求证：CD⊥PD；

（Ⅱ）求证：BD⊥平面PAB；

（Ⅲ）在棱PD上是否存在点M，使CM∥平面PAB，若存在，确定点M的位置，若不存在，请说明理由.

Answer 1

【答案】（Ⅰ）详见解析；（Ⅱ）详见解析；（Ⅲ）在棱PD上存在点M，使CM∥平面PAB，且M是PD的中点.

【解析】

（Ⅰ）由题意可得CD⊥平面PAD，从而易得CD⊥PD；

（Ⅱ）要证BD⊥平面PAB，关键是证明；

（Ⅲ）在棱PD上存在点M，使CM∥平面PAB，且M是PD的中点.

（Ⅰ）证明：因为PA⊥平面ABCD，平面ABCD

所以CD⊥PA.

因为CD⊥AD，，

所以CD⊥平面PAD.

因为平面PAD，

所以CD⊥PD.

(II)因为PA⊥平面ABCD，平面ABCD

所以BD⊥PA.

在直角梯形ABCD中，，

由题意可得，

所以，

所以.

因为，

所以平面PAB.

（Ⅲ）解：在棱PD上存在点M，使CM∥平面PAB，且M是PD的中点.

证明：取PA的中点N，连接MN，BN，

因为M是PD的中点，所以.

因为，所以.

所以MNBC是平行四边形，

所以CM∥BN.

因为平面PAB, 平面PAB.

所以平面PAB.