题目内容

求值：sin
13
3
π=
 
．
考点：运用诱导公式化简求值
专题：三角函数的求值
分析：利用诱导公式化简sin
13
3
π=sin
π
3
，即可求得答案．
解答： 解：sin
13
3
π=sin（4π+
π
3
）=sin
π
3
=
3
2
，
故答案为：
3
2
．
点评：本题考查运用诱导公式化简求值，属于基础题．
练习册系列答案
相关题目
过双曲线
x2
a2
-
y2
b2
=1（a＞0，b＞0）的一个焦点F作渐近线的垂线，垂直为M，延长FM交y轴于E．若
FE
=λ
FM
（1＜λ＜2），则该双曲线的离心率的取值范围为（　　）
A、（1，2）
B、（2，+∞）
C、（1，
2
）
D、（
2
，+∞）
已知函数f（x）=2asinxcosx+
3
cos2x-
3
sin2x，且f（
π
3
）=0．
（1）求a的值及f（x）的最小正周期；
（2）当x∈[-
π
3
，
π
6
]时，求f（x）的值域．
设a＞0，两个函数f（x）=eax，g（x）=blnx的图象关于直线y=x对称．
（1）求实数a，b满足的关系式；
（2）当a=1时，在（
1
2
，+∞）上解不等式f（1-x）+g（x）＜x2．
（3）试指出函数h（x）=f（x）-g（x）在（0，
1
e
]的零点个数，并给出证明．
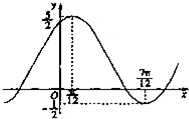
函数y=Asin（ωx+Φ）+k（A＞0，ω＞0，|Φ|＜
π
2
）的图象如图所示，则y的表达式是（　　）
A、y=
3
2
sin（2x+
π
3
）+1
B、y=
3
2
sin（2x-
π
3
）+1
C、y=
3
2
sin（2x+
π
3
）-1
D、y=sin（2x+
π
3
）+1
已知函数f（x）=2x-2-x，数列{an}满足f（log2an）=-2n．
（1）求数列{an}的通项公式；
（2）求证：数列{an}是递减数列．
已知定义在R上的函数f（x）在[-4，+∞）上为增函数，且y=f（x-4）是偶函数，则f（-6），f（-4），f（0）的大小关系为
 
（从小到大用“＜”连接）
已知函数f（x）=
(1-2a)x，x≤1
logax+
1
3
，		x＞1
，当x1≠x2时，
f(x1)-f(x2)
x1-x2
＜0，则a的取值范围是（　　）
A、（0，
1
3
]
B、[
1
3
，
1
2
]
C、（0，
1
2
]
D、[
1
4
，
1
3
]
用反证法证明命题“三角形的内角中至少有一个不大于60°”时，反设正确的是（　　）
A、假设三内角至多有两个大于60°
B、假设三内角都不大于60°
C、假设三内角至多有一个大于60°
D、假设三内角都大于60°

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网