题目内容
10.若直线y=x-b与曲线$\left\{\begin{array}{l}{x=2+cosθ}\\{y=sinθ}\end{array}\right.$(θ为参数)有两个不同的公共点,求实数b的取值范围.分析 求出曲线的普通方程,由公共点个数可知直线与圆相交,求出圆心到直线的距离d,令d<r解不等式得出b的范围.
解答 解:曲线$\left\{\begin{array}{l}{x=2+cosθ}\\{y=sinθ}\end{array}\right.$的普通方程为(x-2)2+y2=1.
∴曲线的圆心为A(2,0),半径为1.
直线y=x-b的一般方程为x-y-b=0.
∵直线与曲线有两个不同的公共点,
∴圆心A(2,0)到直线l的距离d<1.
∴$\frac{|2-b|}{\sqrt{2}}<1$,解得2-$\sqrt{2}$<b<2+$\sqrt{2}$.
点评 本题考查了参数方程与普通方程的转化,直线与圆的位置关系.属于基础题.

练习册系列答案
相关题目
19.$\frac{3π}{5}$弧度化为角度是( )
| A. | 110° | B. | 160° | C. | 108° | D. | 218° |
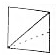
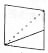
 如图所示,将图(1)中的正方体截去两个三棱锥,得到图(2)中的几何体,则该几何体的侧视图是( )
如图所示,将图(1)中的正方体截去两个三棱锥,得到图(2)中的几何体,则该几何体的侧视图是( )

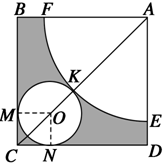 如图所示,在边长为$5+\sqrt{2}$的正方形ABCD中,以A为圆心画一个扇形,以O为圆心画一个圆,M,N,K为切点,以扇形为圆锥的侧面,以圆O为圆锥底面,围成一个圆锥,求圆锥的表面积与体积.
如图所示,在边长为$5+\sqrt{2}$的正方形ABCD中,以A为圆心画一个扇形,以O为圆心画一个圆,M,N,K为切点,以扇形为圆锥的侧面,以圆O为圆锥底面,围成一个圆锥,求圆锥的表面积与体积.