题目内容

式子log2（log2（log24））=
 
．
考点：对数的运算性质
专题：函数的性质及应用
分析：利用对数的性质求解．
解答： 解：log2（log2（log24））
=log2（log22）
=log21
=0．
故答案为：0．
点评：本题考查对数值的求法，是基础题，解题时要认真审题，注意函数性质的合理运用．
练习册系列答案
相关题目
已知一个空间几何体的三视图如图所示，根据图中标出的尺寸（单位：cm），可得这个几何体的体积是（　　）
A、8B、12C、16D、24
若关于x，y的方程组
ax+by=1
x2+y2=10
有解，且所有的解都是整数，则有序数对（a，b）的数目为
 
．
在集合{a，b，c，d}上定义两种运算如下：
⊕abcd?abcd
aabcdaaaaa
bbbbbbabcd
ccbcbcacca
ddbbddadad
那么d?（a⊕c）=（　　）
A、aB、bC、cD、d
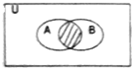已知全集U=R，集合A={y|y=sinx，x∈R}和B={x|x2-x＜0}的关系的韦恩图（vean）如图所示，则阴影部分表示的集合是（　　）
A、{x|-1≤x＜1}
B、{x|-1＜x＜1}
C、{x|0＜x＜1}
D、{x|0＜x≤1}
下列各组中两个函数是同一函数的是（　　）
A、f(x)=
x2-1
x-1
与g（x）=x+1
B、f（r）=πr2（r≥0）与g（x）=πx2（x≥0）
C、f(x)=logaax(a＞0，且a≠1）与g(x)=alogax(a＞0，且a≠1)
D、f(x)=|x|与g(t)=(
t
)2
已知f（x）=mx2+（1-3m）x+2m-1．
（Ⅰ）设m=2时，f（x）≤0的解集为A，集合B=（a，2a+1]（a＞0）．若A⊆B，求a的取值范围；
（Ⅱ）求关于x的不等式f（x）≤0的解集S；
（Ⅲ）若存在x＞0，使得f（x）＞-3mx+m-1成立，求实数m的取值范围．
已知全集U={1，2，3，4，5，6}，集合A={1，3，4，6}，则集合∁UA的所有子集共有
 
个．
若集合A={x|x＞-1}，则以下关系中正确的是（　　）
A、0?AB、{0}∈A
C、0∉AD、{0}?A

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网