题目内容
8.若关于x的不等式-x2+x>mx的解集为{x|-1<x<0},则二项式(1+mx)2016的展开式中的x系数为4032.分析 根据一元二次不等式的解集求得m=2,再利用二项展开式的通项公式求得展开式中的x系数.
解答 解:关于x的不等式-x2+x>mx,即x2+(m-1)x<0,即x(x+m-1)<0,它的解集为{x|-1<x<0},
∴1-m=-1,∴m=2,
则二项式(1+mx)2016=(1+2x)2016的展开式的通项公式为Tr+1=${C}_{2016}^{r}$•(2x)r,
令r=1,可得x系数为2016•2=4032,
故答案为:4032.
点评 本题主要考查一元二次不等式的解法,二项式定理的应用,二项展开式的通项公式,属于基础题.

练习册系列答案
相关题目
3.已知集合M={x|0<x<2},N={x|x>1},则M∩(∁RN)=( )
| A. | (0,1] | B. | [0,1) | C. | (1,2) | D. | [1,2) |
20.已知集合M={x||x|≤2,x∈R},N={x||x-1|≤a,a∈R},若N⊆M,则a的取值范围为( )
| A. | 0≤a≤1 | B. | a≤1 | C. | a<1 | D. | 0<a<1 |
18.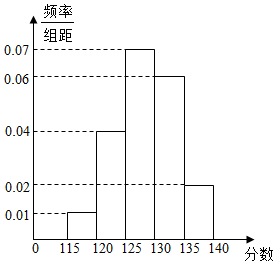 某校在一次高三年级“诊断性”测试后,对该年级的500名考生的成绩进行统计分析,成绩的频率分布表及频率分布直方图如图所示,规定成绩不小于125分为优秀.
某校在一次高三年级“诊断性”测试后,对该年级的500名考生的成绩进行统计分析,成绩的频率分布表及频率分布直方图如图所示,规定成绩不小于125分为优秀.
(1)若用分层抽样的方法从这500人中抽取20人的成绩进行分析,求其中成绩为优秀的学生人数;
(2)在(1)中抽取的20名学生中,要随机抽取2名学生参加分析座谈会,记其中成绩为优秀的人数为X,求X的分布列及数学期望.
 某校在一次高三年级“诊断性”测试后,对该年级的500名考生的成绩进行统计分析,成绩的频率分布表及频率分布直方图如图所示,规定成绩不小于125分为优秀.
某校在一次高三年级“诊断性”测试后,对该年级的500名考生的成绩进行统计分析,成绩的频率分布表及频率分布直方图如图所示,规定成绩不小于125分为优秀.(1)若用分层抽样的方法从这500人中抽取20人的成绩进行分析,求其中成绩为优秀的学生人数;
(2)在(1)中抽取的20名学生中,要随机抽取2名学生参加分析座谈会,记其中成绩为优秀的人数为X,求X的分布列及数学期望.
| 区间 | 人数 |
| [115,120) | 25 |
| [120,125) | a |
| [125,130) | 175 |
| [130,135) | 150 |
| [135,140) | b |