题目内容

2．有6名同学站成一排，求：
（1）总共有多少种不同的排法；
（2）甲、乙、丙不相邻有多少种不同的排法．

分析 （1）求出6名同学的全排列即可；
（2）先将其余3名同学全排列，形成4个空，再进行插入，可得不同的排法．

解答 解：（1）6名同学的全排列=${A}_{6}^{6}$=720；
（2）先将其余3名同学全排列，形成4个空，再进行插入，可得不同的排法$A_3^3A_4^3=144$种．

点评 本题考查排列知识的运用，考查插空法，考查学生的计算能力，属于中档题．

练习册系列答案
相关题目
2．设数列{an}是公差不为零的等差数列，且a1，a3，a7构成等比数列，则公比q为（　　）
A．$\sqrt{2}$B．4C．2D．$\frac{1}{2}$
3．已知等差数列{an}，（n∈N*）满足a1=2，a7=14．
（1）求该数列的公差d和通项公式an；
（2）设Sn为数列{an}的前n项和，若Sn≥3n+15，求n的取值范围．
10．设函数f（x）的定义域为R，f（-x）=f（x），f（x）=f（2-x），当x∈[0，1]时，f（x）=x3．则函数g（x）=|cos（πx）|-f（x）在区间[-$\frac{1}{2}$，$\frac{5}{2}$]上的所有零点的和为（　　）
A．7B．6C．3D．2
17．平面直角坐标系中，点（-2，t）在直线x-2y+4=0左上方，则t的取值范围是t＞1．
7．将参数方程$\left\{\begin{array}{l}x=t+\frac{1}{t}\\ y={t^2}+\frac{1}{t^2}\end{array}\right.$（t为参数）化为普通方程为x2-y-2=0（y≥2）．
14．下列有关命题的叙述，错误的个数为（　　）
（1）若p∨q为真命题，则p∧q为真命题；
（2）命题“若x2-3x+2=0，则x=1或x=2”的逆否命题为“若x≠1或x≠2，则x2-3x+2≠0”；
（3）命题“若a＞b，则$\frac{1}{a}＜\frac{1}{b}$”为真命题；
（4）命题：“若am2≤bm2，则a≤b”的否命题为真．
A．1个B．2个C．3个D．4个
11．在△ABC中，a，b，c分别是角A，B，C的对边，已知3（b2+c2）=3a2+2bc．
（1）求sinA的值；
（2）若a=2，△ABC的面积S=$\frac{{\sqrt{2}}}{2}$，且b＞c，求b和c的值．
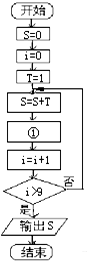12．如图是在求：S=1+$\frac{1}{2}$+$\frac{1}{2^2}$+$\frac{1}{2^3}$+…+的一个程序框图．
（1）在程序框图的①处填上适当的语句．
（2）写出相应的程序．
答：（1）T=T/2；
（2）S=0
I=0
T=1
DO
S=S+T
T=T/2
I=I+1
LOOPUNTILI＞9
PRINTS
END．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网