题目内容

10．一个样本a，3，5，7的平均数是b，且a，b分别是数列{2n-2}（n∈N*）的第2项和第4项，则这个样本的方差是（　　）
A．3B．4C．5D．6

分析 由已知条件求出a=1，b=4，由此能求出S2．

解答 解：∵样本a，3，5，7的平均数是b，且a，b分别是数列{2n-2}（n∈N*）的第2项和第4项，
∴a=22-2=1，b=24-2=4，
∴S2=$\frac{1}{4}$[（1-4）2+（3-4）2+（5-4）2+（7-4）2]=5，
故选：C．

点评 本题考查样本方差的求法，是基础题，解题时要认真审题，注意数列、平均数、方差性质的合理运用．

练习册系列答案
相关题目
9．若${∫}_{1}^{m}$（2x-1）dx=6（其中m＞1），则二项式（x-$\frac{1}{x}$）m展开式中含x项的系数为-3．
1．已知函数f（x）=sinωx+$\sqrt{3}$cosωx（ω＞0）在区间（0，π）上存在3个不同的x0，使得f（x0）=1，则ω的取值范围为（　　）
A．（$\frac{5}{2}$，$\frac{23}{6}$]B．（$\frac{5}{2}$，$\frac{23}{6}$）C．（$\frac{3}{2}$，$\frac{19}{6}$）D．（$\frac{3}{2}$，$\frac{19}{6}$]
18．已知△ABC的三边|AB|=$\sqrt{13}$，|BC|=4，|AC|=1，动点M满足$\overrightarrow{CM}=λ\overrightarrow{CA}+μ\overrightarrow{CB}$，且λμ=$\frac{1}{4}$．
（1）求cos∠ACB；
（2）求|$\overrightarrow{CM}$|的最小值．
5．已知数列{an}是等差数列，Sn是其前n项和，a1=2，S3=12．
（1）求数列{an}的通项公式； 
（2）设bn=an+4n，求数列{bn}的前n项和Tn．
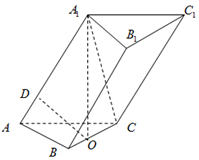15．三棱柱ABC-A1B1C1的底面ABC是等边三角形，BC的中点为O，A1O⊥底面ABC，AA1与底面ABC所成的角为$\frac{π}{3}$，点D在棱AA1上，且AD=$\sqrt{3}$，AB=4．
（1）求证：OD⊥平面BB1C1C；
（2）求二面角B-B1C-A1的平面角的余弦值．
2．已知函数f（x）=2lnx-x2
（1）讨论f（x）的单调性并求最大值；
（2）设g（x）=xex-（a-1）x2-x-2lnx，若f（x）+g（x）≥0恒成立，求实数a的取值范围．
19．在（x2-4）（x+$\frac{1}{x}$）9的展开式中x5的系数为（　　）
A．36B．-144C．60D．-60
20．已知集合A={x|-3＜2x+1＜7}，集合B={x|y=log2（x-1）}，集合C={x|x＜a+1}．
（Ⅰ）求A∩B．
（Ⅱ）设全集为R，若∁R（A∪B）⊆C，求实数a的取值范围．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网