题目内容
5.已知数列{an}是等差数列,Sn是其前n项和,a1=2,S3=12.(1)求数列{an}的通项公式;
(2)设bn=an+4n,求数列{bn}的前n项和Tn.
分析 (1)将已知条件转化为首项和公差表示,解方程组可求得基本量的值,从而确定通项公式;
(2)首先化简数列{bn}的通项公式,结合特点采用分组求和法求解.
解答 解:(1)∵a1=2,S3=12.
∴3×2+3d=12,解得d=2.
∴an=2+2(n-1)=2n.
(2)∵${b_n}={a_n}+{4^n}=2n+{4^n}$,
Tn=2(1+2+…+n)+(4+42+…+4n)
=$2×\frac{n(1+n)}{2}$+$\frac{4({4}^{n}-1)}{4-1}$
=n2+n+$\frac{{4}^{n+1}-4}{3}$.
点评 本题考查了等差数列与等比数列的通项公式与求和公式、分组求和方法,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
5.若至少存在一个x≥0,使得关于x的不等式x2≤4-|2x+m|成立,则实数m的取值范围是( )
| A. | [-4,5] | B. | [-5,5] | C. | [4,5] | D. | [-5,4] |
20.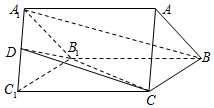 如图,在三棱柱ABC-A1B1C1中,△ABC是等边三角形,BC=CC1,D是A1C1中点.
如图,在三棱柱ABC-A1B1C1中,△ABC是等边三角形,BC=CC1,D是A1C1中点.
(Ⅰ)求证:A1B∥平面B1CD;
(Ⅱ)当三棱锥C-B1C1D体积最大时,求点B到平面B1CD的距离.
 如图,在三棱柱ABC-A1B1C1中,△ABC是等边三角形,BC=CC1,D是A1C1中点.
如图,在三棱柱ABC-A1B1C1中,△ABC是等边三角形,BC=CC1,D是A1C1中点.(Ⅰ)求证:A1B∥平面B1CD;
(Ⅱ)当三棱锥C-B1C1D体积最大时,求点B到平面B1CD的距离.
17.已知函数$f(x)=\left\{\begin{array}{l}x(x+4),x≥0\\ x(x-4),x<0\end{array}\right.$,则f(-3)=( )
| A. | -3 | B. | 21 | C. | 3 | D. | -21 |
14.已知函数f(x)满足下列条件:①定义域为[1,+∞);②当1<x≤2时f(x)=4sin($\frac{π}{2}$x);③f(x)=2f(2x).若关于x的方程f(x)-kx+k=0恰有3个实数解,则实数k的取值范围是( )
| A. | $[\frac{1}{14},\frac{1}{3})$ | B. | $(\frac{1}{14},\frac{1}{3}]$ | C. | $(\frac{1}{3},2]$ | D. | $[\frac{1}{3},2)$ |
15.在平面直角坐标系中,角α的终边经过点(-$\frac{1}{2}$,$\frac{\sqrt{3}}{2}$),则sinα的值为( )
| A. | $\frac{1}{2}$ | B. | -$\frac{1}{2}$ | C. | -$\frac{\sqrt{3}}{2}$ | D. | $\frac{\sqrt{3}}{2}$ |