题目内容
我们给出如下定义:对函数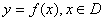 ,若存在常数
,若存在常数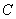 (
(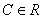 ),对任意的
),对任意的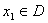 ,存在唯一的
,存在唯一的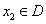 ,使得
,使得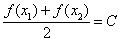 ,则称函数
,则称函数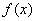 为“和谐函数”,称常数
为“和谐函数”,称常数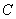 为函数
为函数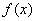 的 “和谐数”.
的 “和谐数”.
(Ⅰ)判断函数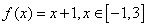 是否为“和谐函数”?答: . 是(填“是”或“否”)如果是,写出它的一个“和谐数”: .
是否为“和谐函数”?答: . 是(填“是”或“否”)如果是,写出它的一个“和谐数”: .
(Ⅱ)请先学习下面的证明方法:
证明:函数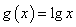 ,
,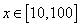 为“和谐函数”,
为“和谐函数”, 是其“和谐数”;
是其“和谐数”;
证明过程如下:对任意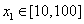 ,令
,令 ,即
,即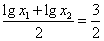 ,
,
得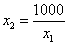 .∵
.∵ 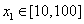 ,∴
,∴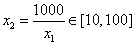 .
.
即对任意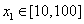 ,存在唯一的
,存在唯一的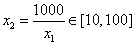 ,使得
,使得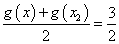 .
.
∴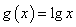 为“和谐函数”,其“和谐数”为
为“和谐函数”,其“和谐数”为 .
.
参照上述证明过程证明:函数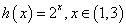 为“和谐函数”,
为“和谐函数”,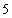 是其“和谐数”;
是其“和谐数”;
[证明]:
(III)判断函数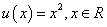 是否为和谐函数,并作出证明.
是否为和谐函数,并作出证明.
解: (1)是,C=2
(2)对任意 ,令
,令 ,即
,即 ,得
,得 ,
,
 .∵
.∵  ,∴
,∴  ,
, .
.
即对任意 ,存在唯一的
,存在唯一的 ,使得
,使得 .
.
∴  为“和谐函数”,
为“和谐函数”,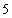 是其“和谐数”.
是其“和谐数”.
(3)对任意的常数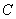 ,
,
ⅰ)若 ,则对于
,则对于 ,显然不存在
,显然不存在 ,使得
,使得 成立,
成立,
所以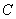
 不是函数
不是函数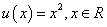 的和谐数;-
的和谐数;-
ⅱ) 若 ,则对于
,则对于 ,由
,由 得,
得, ,
,
即不存在 ,使
,使 成立.
成立.
所以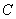
 也不是函数
也不是函数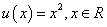 的和谐数.
的和谐数.
综上所述,函数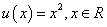 不是“和谐函数”.
不是“和谐函数”.
{或者借助唯一来否定也可,按步骤酌情给分。}

练习册系列答案
相关题目
 的展开式中,第
的展开式中,第 项的二项式系数与第
项的二项式系数与第 项的二项式系数之比是
项的二项式系数之比是 .
. 项的系数;
项的系数; 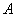 :“取出的2件产品中至多有1件是二等品”的概率
:“取出的2件产品中至多有1件是二等品”的概率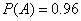 .
.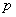 ;
; 对边分别为
对边分别为 ,
, ,则角
,则角 的值为 .
的值为 .  的图像大致为 ( )
的图像大致为 ( ) 

 ,则△ABC的形状是( )
,则△ABC的形状是( ) ,其中
,其中 .
. 在
在 处取得极值,求
处取得极值,求 的值;
的值;