题目内容
已知数列{an},对任何正整数n都有:a1•1+a2•2+a3•22+…+an•2n-1=(n-1)•2n+1.
(1)求数列{an}的通项公式;
(2)①若λ≥
(n∈N+)恒成立,求实数λ的范围;
②若数列{bn}满足bn=|(-1)n•2an+7-2an|,求数列{bn}的前项和Sn.
(1)求数列{an}的通项公式;
(2)①若λ≥
| 7an-2 |
| 2an |
②若数列{bn}满足bn=|(-1)n•2an+7-2an|,求数列{bn}的前项和Sn.
考点:数列的求和,数列递推式
专题:等差数列与等比数列
分析:(1)设bn=2n-1,由a1b1+a2b2+a3b3+…+an-1bn-1+anbn=(n-1)•2n+1,得an•bn=n•2n-1,从而能求出数列{an}的通项公式.
(2)①记f(n)=
,n∈N*,则
=
•
=
(1+
),推导出f(n)先增后减,在n=2时取到最大值,由此求出λ≥f(2)=3.
②由bn=|(-1)n•2n+7-2n|=|(-1)n(7-2n)+2n|,得到Sn=(5-2)+(3+22)+(-1+23)+(-1+24)+(3+25)+(-5+26)+…+[(-1)n(7-2n)+2n],由此能求出数列{bn}的前项和Sn.
(2)①记f(n)=
| 7n-2 |
| 2n |
| f(n+1) |
| f(n) |
| 1 |
| 2 |
| 7n-5 |
| 7n-2 |
| 1 |
| 2 |
| 5 |
| 7n-2 |
②由bn=|(-1)n•2n+7-2n|=|(-1)n(7-2n)+2n|,得到Sn=(5-2)+(3+22)+(-1+23)+(-1+24)+(3+25)+(-5+26)+…+[(-1)n(7-2n)+2n],由此能求出数列{bn}的前项和Sn.
解答:
解:(1)依题意,设数列{bn}的通项公式为bn=2n-1,
由a1b1+a2b2+a3b3+…+an-1bn-1+anbn=(n-1)•2n+1,
可得a1b1+a2b2+a3b3+…+an-1bn-1=(n-2)•2n-1+1(n≥2),
两式相减可得an•bn=n•2n-1,即an=n.
当n=1时,a1=1,从而对一切n∈N*,都有an=n.
∴数列{an}的通项公式是an=n.
(2)①记f(n)=
,n∈N*,
则
=
•
=
(1+
),
当n=1时,
>1,f(2)>f(1),
当n≥2时,
≤
(1+
)<1,
∴f(n)先增后减,在n=2时取到最大值,
∴λ≥f(2)=3.
②bn=|(-1)n•2an+7-2an|=|(-1)n•2n+7-2n|=|(-1)n(7-2n)+2n|,
Sn=(5-2)+(3+22)+(-1+23)+(-1+24)+(3+25)+(-5+26)+…+[(-1)n(7-2n)+2n]
=5-2+3-1+(22+23+24+…+2n)+[-1+3-5+7-9+…+(-1)n(7-2n)]
=3+(2+22+23+24+…+2n)+[-1+3-5+7-9+…+(-1)n(7-2n)]
=
=
.
由a1b1+a2b2+a3b3+…+an-1bn-1+anbn=(n-1)•2n+1,
可得a1b1+a2b2+a3b3+…+an-1bn-1=(n-2)•2n-1+1(n≥2),
两式相减可得an•bn=n•2n-1,即an=n.
当n=1时,a1=1,从而对一切n∈N*,都有an=n.
∴数列{an}的通项公式是an=n.
(2)①记f(n)=
| 7n-2 |
| 2n |
则
| f(n+1) |
| f(n) |
| 1 |
| 2 |
| 7n-5 |
| 7n-2 |
| 1 |
| 2 |
| 5 |
| 7n-2 |
当n=1时,
| f(n+1) |
| f(n) |
当n≥2时,
| f(n+1) |
| f(n) |
| 1 |
| 2 |
| 5 |
| 12 |
∴f(n)先增后减,在n=2时取到最大值,
∴λ≥f(2)=3.
②bn=|(-1)n•2an+7-2an|=|(-1)n•2n+7-2n|=|(-1)n(7-2n)+2n|,
Sn=(5-2)+(3+22)+(-1+23)+(-1+24)+(3+25)+(-5+26)+…+[(-1)n(7-2n)+2n]
=5-2+3-1+(22+23+24+…+2n)+[-1+3-5+7-9+…+(-1)n(7-2n)]
=3+(2+22+23+24+…+2n)+[-1+3-5+7-9+…+(-1)n(7-2n)]
=
|
=
|
点评:本题主要考查数列的通项公式的求法、前n项和公式的求法,考查等差数列、等比数列等基础知识,考查抽象概括能力,推理论证能力,运算求解能力,考查化归与转化思想、函数与方程思想,解题时要注意分组求和法的合理运用.

练习册系列答案
相关题目
函数y=x(|x|-1)的图象是( )
A、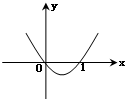 |
B、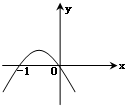 |
C、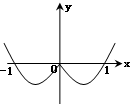 |
D、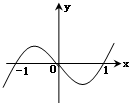 |
若
=
,则tan2α=( )
| 1+cos2α |
| sin2α |
| 1 |
| 2 |
A、
| ||
B、-
| ||
C、
| ||
D、-
|
三角函数f(x)=asinx-bcosx,若f(
-x)=f(
+x),则直线ax-by+c=0的倾斜角为( )
| π |
| 4 |
| π |
| 4 |
A、
| ||
B、
| ||
C、
| ||
D、
|
设0<α<
,a是大于0的常数,函数F(α)=
+
,若F(α)≥16恒成立,则a的取值范围是( )
| π |
| 2 |
| 1 |
| cosα |
| a |
| 1-cosα |
| A、[1,+∞) |
| B、[4,+∞) |
| C、(9,+∞) |
| D、[9,+∞) |