题目内容
13.下列函数是偶函数,且最小正周期为π的是( )| A. | y=sin(π-2x) | B. | y=sin2xcos2x | C. | y=cos22x+1 | D. | y=cos(2x-π) |
分析 根据正弦型函数及余弦型函数的性质,我们逐一分析四个答案中的四个函数的周期性及奇偶性,然后和题目中的条件进行比照,即可得到答案.
解答 D解:A中,函数y=sin(π-2x)=sin2x为奇函数,不满足条件;
B中,函数y=sin2xcos2x=$\frac{1}{2}$sin4x周期为$\frac{π}{2}$,不满足条件;
C中,函数y=cos22x+1=$\frac{1}{2}$cos4x+$\frac{3}{2}$周期为$\frac{π}{2}$,不满足条件;
D中,函数y=cos(2x-π)=-cos2x是最小正周期为π的偶函数,满足条件;
故选:D.
点评 本题考查的知识点是正弦(余弦)函数的奇偶性,三角函数的周期性及其求法,熟练掌握正弦型函数及余弦型函数的性质是解答本题的关键.

练习册系列答案
 英才计划期末调研系列答案
英才计划期末调研系列答案
相关题目
1.已知f0(x)=cosxsinx,f1(x)=f0′(x),f2(x)=f1′(x),f3(x)=f2′(x),fn(x)=fn-1′(x),n∈N+,则f2016(x)等于( )
| A. | sin22015x | B. | 2cosxsinx | C. | -22015cos2x | D. | 22015sin2x |
4.已知正方形ABCD的面积为2,点P在边AB上,则$\overrightarrow{PD}$•$\overrightarrow{PC}$的最大值为( )
| A. | $\frac{\sqrt{6}}{2}$ | B. | $\frac{3}{2}$ | C. | 2 | D. | $\sqrt{2}$ |
5.函数f(x)=Asin(ωx+φ)的部分图象如图所示,则函数的解析式可以是( )
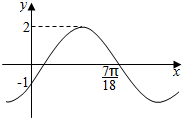

| A. | f(x)=2cos(3x+$\frac{2π}{3}$) | B. | f(x)=2sin($\frac{15}{7}x-\frac{5π}{6}$) | ||
| C. | f(x)=2sin(3x-$\frac{π}{6}$) | D. | f(x)=2sin(3x-$\frac{π}{6}$)或f(x)=2sin($\frac{15}{7}x-\frac{5π}{6}$) |
2.设f(x)=x+sinx(x∈R),则下列说法错误的是( )
| A. | f(x)是奇函数 | B. | f(x)在R上单调递增 | C. | f(x)的值域为R | D. | f(x)是周期函数 |