题目内容
3.对a>0且a≠1的所有正实数,函数y=loga(2x-3)+$\frac{\sqrt{2}}{2}$的图象恒过定点P,P在幂函数f(x)的图象上,则f(9)=$\frac{1}{3}$.分析 根据对数函数的图象和性质,可得定点P坐标(2,$\frac{\sqrt{2}}{2}$),进而根据P在幂函数f(x)的图象上,可得幂函数f(x)的解析式,将x=9代入可得答案.
解答 解:令2x-3=1,则x=2,y=$\frac{\sqrt{2}}{2}$恒成立,
故函数y=loga(2x-3)+$\frac{\sqrt{2}}{2}$的图象恒过定点P(2,$\frac{\sqrt{2}}{2}$),
若P在幂函数f(x)=xa的图象上,
∴2a=$\frac{\sqrt{2}}{2}$,
∴a=-$\frac{1}{2}$,即f(x)=${x}^{-\frac{1}{2}}$,
∴f(9)=$\frac{1}{3}$,
故答案为:$\frac{1}{3}$
点评 本题考查的知识点是对数函数的图象与性质,幂函数的图象和性质,难度中档.

练习册系列答案
 计算高手系列答案
计算高手系列答案
相关题目
8.在数列{an}中,已知a1=3,当n≥2时,$\frac{1}{a_n}-\frac{1}{{{a_{n-1}}}}=\frac{1}{5},{a_{16}}$=( )
| A. | $\frac{2}{5}$ | B. | $\frac{3}{10}$ | C. | $\frac{2}{3}$ | D. | $\frac{3}{2}$ |
13.直线y=mx+2过双曲线$\frac{{x}^{2}}{2}$-y2=1的顶点,则m等于( )
| A. | 0 | B. | ±$\sqrt{2}$ | C. | ±$\frac{\sqrt{2}}{2}$ | D. | ±$\frac{1}{2}$ |

 B.
B. C.
C. D.
D.
 的直线与椭圆
的直线与椭圆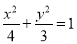 交于
交于 两点, 且点
两点, 且点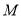 平分弦
平分弦 ,则直线
,则直线 的方程为( )
的方程为( ) B.
B. 
 D.
D. 