题目内容
三个数cos
,sin
,-cos
的大小关系是( )
| 3 |
| 2 |
| 1 |
| 10 |
| 7 |
| 4 |
A、cos
| ||||||
B、cos
| ||||||
C、cos
| ||||||
D、-cos
|
考点:终边相同的角,余弦函数的图象
专题:三角函数的求值
分析:先利用诱导公式,再利用余弦函数在(0,
)上单调递减,即可得出结论.
| π |
| 2 |
解答:
解:由题意-cos
=cos(π-
),sin
=cos(
-
)
∵0<π-
<
-
<
<
,余弦函数在(0,
)上单调递减,
∴cos(π-
)>cos(
-
)>cos
∴cos
<sin
<-cos
故选:C.
| 7 |
| 4 |
| 7 |
| 4 |
| 1 |
| 10 |
| π |
| 2 |
| 1 |
| 10 |
∵0<π-
| 7 |
| 4 |
| π |
| 2 |
| 1 |
| 10 |
| 3 |
| 2 |
| π |
| 2 |
| π |
| 2 |
∴cos(π-
| 7 |
| 4 |
| π |
| 2 |
| 1 |
| 10 |
| 3 |
| 2 |
∴cos
| 3 |
| 2 |
| 1 |
| 10 |
| 7 |
| 4 |
故选:C.
点评:本题考查诱导公式,余弦函数在(0,
)上单调递减,考查学生的计算能力,属于中档题.
| π |
| 2 |

练习册系列答案
 举一反三单元同步过关卷系列答案
举一反三单元同步过关卷系列答案
相关题目
已知实数x,y满足
,则z=2x+y的最小值是( )
|
| A、1 | B、2 | C、4 | D、8 |
某程序框图如图所示,则输出的结果S=( )
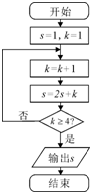

| A、11 | B、26 | C、57 | D、120 |
当x,y满足
时,则t=x+y的最大值是( )
|
| A、1 | B、2 | C、6 | D、5 |
已知对数函数y=logax(a>0且a≠1)的图象经过点(4,
),则a的值是( )
| 1 |
| 2 |
| A、-16 | ||
B、-
| ||
| C、16 | ||
D、
|
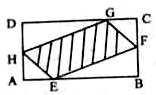 廊坊市某所中学有一块矩形空地,学校要在这块空地上修建一个内接四边形的花坛(如图所示),该花坛的四个顶点分别落在矩形的四条边上,已知 A B=a(a>2),BC=2,且 A E=A H=CF=CG,设 A E=x,花坛面积为y.
廊坊市某所中学有一块矩形空地,学校要在这块空地上修建一个内接四边形的花坛(如图所示),该花坛的四个顶点分别落在矩形的四条边上,已知 A B=a(a>2),BC=2,且 A E=A H=CF=CG,设 A E=x,花坛面积为y.