题目内容
已知函数f(x)=|2x-a|+|2x+3|,g(x)=|x-1|+2.
(1)当a=1,不等式f(x)>m恒成立,求实数的取值范围;
(2)若对任意x1∈R,都有x2∈R使f(x1)=g(x2)成立,求实数a的取值范围.
(1)当a=1,不等式f(x)>m恒成立,求实数的取值范围;
(2)若对任意x1∈R,都有x2∈R使f(x1)=g(x2)成立,求实数a的取值范围.
考点:绝对值不等式的解法,函数恒成立问题
专题:计算题,函数的性质及应用,不等式的解法及应用
分析:(1)运用绝对值不等式的性质,求出F(x)的最小值4,再由不等式恒成立的思想,即可得到m<4;
(2)分别求得f(x)、g(x)的值域,再由值域的包含关系,得到不等式解得即可.
(2)分别求得f(x)、g(x)的值域,再由值域的包含关系,得到不等式解得即可.
解答:
解:(1)当a=1时,f(x)=|2x-1|+|2x+3|=2(|x-
|+|x+
|),
由于|x-
|+|x+
|≥|(x-
)-(x+
)|=2,
当且仅当-
≤x≤
时,取得等号,
则f(x)的最小值为4.
不等式f(x)>m恒成立,即为m<4;
(2)函数f(x)=|2x-a|+|2x+3|≥2|(x-
)-(x+
)|=|a+3|,
即有f(x)的值域为[|a+3|,+∞),
g(x)=|x-1|+2≥2,
则g(x)的值域为[2,+∞).
若对任意x1∈R,都有x2∈R使f(x1)=g(x2)成立,
则[|a+3|,+∞)⊆[2,+∞),
即有|a+3|≥2,解得,a≥-1或a≤-5.
则实数a的取值范围是(-∞,-5]∪[-1,+∞).
| 1 |
| 2 |
| 3 |
| 2 |
由于|x-
| 1 |
| 2 |
| 3 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
当且仅当-
| 3 |
| 2 |
| 1 |
| 2 |
则f(x)的最小值为4.
不等式f(x)>m恒成立,即为m<4;
(2)函数f(x)=|2x-a|+|2x+3|≥2|(x-
| a |
| 2 |
| 3 |
| 2 |
即有f(x)的值域为[|a+3|,+∞),
g(x)=|x-1|+2≥2,
则g(x)的值域为[2,+∞).
若对任意x1∈R,都有x2∈R使f(x1)=g(x2)成立,
则[|a+3|,+∞)⊆[2,+∞),
即有|a+3|≥2,解得,a≥-1或a≤-5.
则实数a的取值范围是(-∞,-5]∪[-1,+∞).
点评:本题考查绝对值不等式的解法和性质,考查不等式的恒成立转化为求函数的最值,考查运算能力,属于中档题和易错题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
2014年11月,北京成功举办了亚太经合组织第二十二次领导人非正式会议,出席会议的有21个国家和地区的领导人或代表.其间组委会安排这21位领导人或代表合影留念,他们站成两排,前排11人,后排10人,中国领导人站在第一排正中间位置,美俄两国领导人站在与中国领导人相邻的两侧,如果对其他领导人或代表所站的位置不做要求,那么不同的排法共有( )
A、
| ||||||
B、
| ||||||
C、
| ||||||
D、
|
已知直线 l过点(1,-1),且在两坐标轴上的截距之和为
,则直线l的力方程为( )
| 3 |
| 2 |
| A、2x-y-3=0 |
| B、2x+y-1=0 |
| C、x-2y-3=0 |
| D、2x+y-1=0或x-2y-3=0 |
已知全集I={0,1,2,3,4},集合M={1,2,3},N={0,3],则(∁IM)∪N=( )
| A、{0,3,4} |
| B、{0} |
| C、{0,1,2,3} |
| D、{0,1,2,3,4} |
已知集合M={x<1},N={x|x>0},则M∩N等于( )
| A、{x|x<1} |
| B、{x|x>1} |
| C、{x|0<x<1} |
| D、∅ |
已知Sn是等差数列{an}的前n项和,若a1=-23,Sn≥0的最小正整数解为n=11,则公差d的取值范围是( )
A、(
| ||||
B、[
| ||||
C、(
| ||||
D、[
|
如图所示,程序框图输出的所有实数对(x,y)所对应的点都在函数( )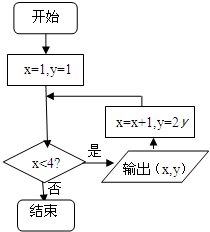

| A、y=x+1的图象上 |
| B、y=2x的图象上 |
| C、y=2x的图象上 |
| D、y=2x-1的图象上 |