题目内容
4.已知向量$\overrightarrow{a}$=(1,-2),$\overrightarrow{a}$⊥$\overrightarrow{b}$,|2$\overrightarrow{a}$-$\overrightarrow{b}$|=5,则|$\overrightarrow{b}$|=$\sqrt{5}$.分析 由条件容易得出${\overrightarrow{a}}^{2}=5,\overrightarrow{a}•\overrightarrow{b}=0$,这样对$|2\overrightarrow{a}-\overrightarrow{b}|=5$的两边同时平方即可求出${\overrightarrow{b}}^{2}$的值,进而求出$|\overrightarrow{b}|$的值.
解答 解:$\overrightarrow{a}⊥\overrightarrow{b}$;
∴$\overrightarrow{a}•\overrightarrow{b}=0$,且$|\overrightarrow{a}{|}^{2}=5$;
∴$(2\overrightarrow{a}-\overrightarrow{b})^{2}=4{\overrightarrow{a}}^{2}-4\overrightarrow{a}•\overrightarrow{b}+{\overrightarrow{b}}^{2}$=$20-0+{\overrightarrow{b}}^{2}=25$;
∴${\overrightarrow{b}}^{2}=5$;
∴$|\overrightarrow{b}|=\sqrt{5}$.
故答案为:$\sqrt{5}$.
点评 考查向量坐标的数量积运算,向量垂直的充要条件,以及向量数量积的运算.

练习册系列答案
相关题目
14.设等差数列{an}的前n项和为Sn,Sm-1=13,Sm=0,Sm+1=-15.其中m∈N*且m≥2,则数列{$\frac{1}{{a}_{n}{a}_{n+1}}$}的前n项和的最大值为( )
| A. | $\frac{24}{143}$ | B. | $\frac{1}{143}$ | C. | $\frac{24}{13}$ | D. | $\frac{6}{13}$ |
12.已知函数f(x)=x(a-$\frac{1}{e^x}$),曲线y=f(x)上存在两个不同点,使得曲线在这两点处的切线都与y轴垂直,则实数a的取值范围是( )
| A. | (-e2,+∞) | B. | (-e2,0) | C. | (-$\frac{1}{e^2}$,+∞) | D. | (-$\frac{1}{e^2}$,0) |
9.某程序框图如图所示,则该程序运行后输出的值是( )
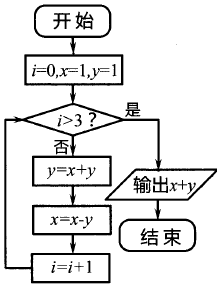

| A. | 0 | B. | -1 | C. | -2 | D. | -8 |
16.已知集合A={x|x2-x+4>x+12},B={x|2x-1<8},则A∩(∁RB)=( )
| A. | {x|x≥4} | B. | {x|x>4} | C. | {x|x≥-2} | D. | {x|x<-2或x≥4} |
13.已知集合A={x|x<-2或x>4},B={x|2x-1<8},则A∩B=( )
| A. | {x|x≥4} | B. | {x|x>4} | C. | {x|x≥-2} | D. | {x|x<-2} |