题目内容
已知抛物线 内一定点E(m,0),(m>0),过点E作斜率分别为k1,k2的两条直线,交抛物线于A、B和C、D,且M,N分别是线段AB、CD的中点.
内一定点E(m,0),(m>0),过点E作斜率分别为k1,k2的两条直线,交抛物线于A、B和C、D,且M,N分别是线段AB、CD的中点.
(1)若m=1,k1= 时,求弦|AB|的长度;
时,求弦|AB|的长度;
(2)若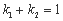 ,判断直线MN是否过定点?并说明理由。
,判断直线MN是否过定点?并说明理由。
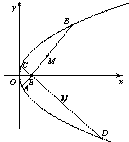
.解:(1)当m=1,则E(1,0)为抛物线焦点,即AB为抛物线的一条焦点弦,
法一: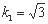 设AB:
设AB: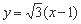 ,则|AB|=x1+x2+p=x1+x2+2
,则|AB|=x1+x2+p=x1+x2+2
联立: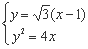 得:
得: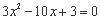 ∴
∴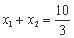 则|AB|=x1+x2+2=
则|AB|=x1+x2+2=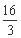
法二: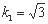 ,则直线倾斜角θ=60°,则|AB|=
,则直线倾斜角θ=60°,则|AB|=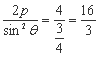
(2) 设AB: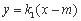
联立: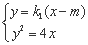 得:
得: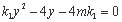 则M为(
则M为(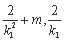 ) 同理:N为(
) 同理:N为(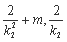 )
)
若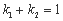 ,则M为(
,则M为(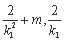 ) N为(
) N为(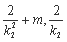 ),kMN=
),kMN=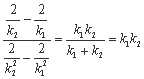
直线MN为: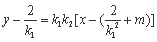 化为:
化为: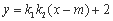 过点(m,2)
过点(m,2)

练习册系列答案
 赢在课堂名师课时计划系列答案
赢在课堂名师课时计划系列答案 天天向上课时同步训练系列答案
天天向上课时同步训练系列答案 阳光课堂同步练习系列答案
阳光课堂同步练习系列答案
相关题目
 与椭圆
与椭圆 有一个共同的焦点,则
有一个共同的焦点,则 =( )
=( ) B.
B.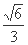 C.
C.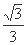 D.
D.
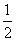 B.
B.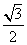 C.
C.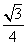 D.
D.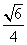
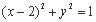 ,那么
,那么 的取值范围是 ;
的取值范围是 ; :
: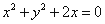 与圆
与圆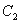 :
: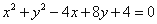 的位置关系是( )
的位置关系是( )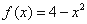 ,
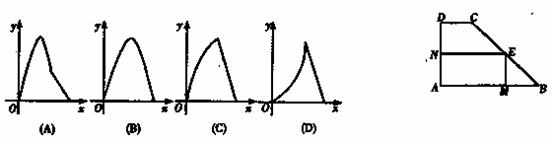
,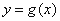 是定义在R上的奇函数,当
是定义在R上的奇函数,当 时,
时,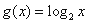 ,则函数
,则函数 的大致图象为( )
的大致图象为( )
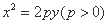 的焦点
的焦点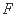 作倾斜角为
作倾斜角为 的直线与抛物线分别交于
的直线与抛物线分别交于 两点(点
两点(点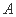 在
在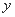 轴右侧),则
轴右侧),则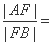 ( )
( ) B、
B、 C、2 D、
C、2 D、
 A=90°,
A=90°, AB于M,EN
AB于M,EN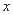 ,矩形AMEN的面积为
,矩形AMEN的面积为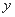 ,那么
,那么