题目内容
已知四棱锥S-ABCD的所有棱长都相等,E是SB的中点,则AE,SD所成的角的正弦值为 ( )
A. B.
B.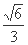 C.
C.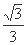 D.
D.
B

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
题目内容
已知四棱锥S-ABCD的所有棱长都相等,E是SB的中点,则AE,SD所成的角的正弦值为 ( )
A. B.
B.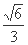 C.
C.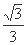 D.
D.
B

 名校课堂系列答案
名校课堂系列答案