题目内容
15.已知动点M到点N(1,0)和直线l:x=-1的距离相等.(Ⅰ)求动点M的轨迹E的方程;
(Ⅱ)已知不与l垂直的直线l'与曲线E有唯一公共点A,且与直线l的交点为P,以AP为直径作圆C.判断点N和圆C的位置关系,并证明你的结论.
分析 (Ⅰ)利用抛物线的定义,即可求动点M的轨迹E的方程;
(Ⅱ)由题意可设直线l':x=my+n,由$\left\{{\begin{array}{l}{x=my+n}\\{{y^2}=4x}\end{array}}\right.$可得y2-4my-4n=0,求出A,P的坐标,利用向量的数量积,即可得出结论.
解答 解:(Ⅰ)设动点M(x,y),
由抛物线定义可知点M的轨迹E是以N(1,0)为焦点,直线l:x=-1为准线的抛物线,
所以轨迹E的方程为y2=4x.
(Ⅱ)点N在以PA为直径的圆C上.
理由:由题意可设直线l':x=my+n,
由$\left\{{\begin{array}{l}{x=my+n}\\{{y^2}=4x}\end{array}}\right.$可得y2-4my-4n=0(*),
因为直线l'与曲线E有唯一公共点A,
所以△=16m2+16n=0,即n=-m2.
所以(*)可化简为y2-4my+4m2=0,
所以A(m2,2m),
令x=-1得$P(-1,-\frac{1+n}{m})$,
因为n=-m2,
所以$\overrightarrow{NA}•\overrightarrow{NP}=({m^2}-1,2m)•(-2,-\frac{1+n}{m})=-2{m^2}+2-2-2n=0$
所以NA⊥NP,
所以点N在以PA为直径的圆C上.
点评 本题考查抛物线的定义与方程,考查直线与抛物线位置关系的运用,考查向量知识,属于中档题.

练习册系列答案
相关题目
5.已知双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1(a,b>0)$的离心率为$\sqrt{5}$,则抛物线x2=4y的焦点到双曲线的渐近线的距离是( )
| A. | $\frac{{\sqrt{5}}}{10}$ | B. | $\frac{{\sqrt{5}}}{5}$ | C. | $\frac{{2\sqrt{5}}}{5}$ | D. | $\frac{{4\sqrt{5}}}{5}$ |
3.二项式$(x-\frac{2}{x}{)^6}$的展开式的第二项是( )
| A. | 6x4 | B. | -6x4 | C. | 12x4 | D. | -12x4 |
20.已知向量$\overrightarrow{a}$=(x,1),$\overrightarrow{b}$=(3,-2),若$\overrightarrow{a}$∥$\overrightarrow{b}$,则x=( )
| A. | -3 | B. | $-\frac{3}{2}$ | C. | $\frac{2}{3}$ | D. | $\frac{3}{2}$ |
5.设i是虚数单位,$\overline{z}$表示复数z的共轭复数,若z=2-i,则z+i$\overline{z}$在复平面内所对应的点位于( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
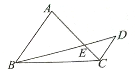 如图所示,AC与BD交于点E,AB∥CD,AC=3$\sqrt{5}$,AB=2CD=6,当tanA=2时,$\overrightarrow{BE}•\overrightarrow{DC}$=-12.
如图所示,AC与BD交于点E,AB∥CD,AC=3$\sqrt{5}$,AB=2CD=6,当tanA=2时,$\overrightarrow{BE}•\overrightarrow{DC}$=-12.