题目内容
13.α,β,γ为不同的平面,a,b,c为三条不同的直线,则下列命题正确的是( )| A. | 若α⊥γ,β⊥γ,则α∥β | B. | 若a∥β,a∥b,则b∥β | ||
| C. | 若a∥α,b∥α,c⊥a,c⊥b,则c⊥α | D. | 若a⊥γ,b⊥γ,则a∥b |
分析 根据空间线面位置关系的判定定理和性质及空间几何体模型进行判断或举反例说明.
解答 解:对于A,当平面α,β,γ两两垂直时,显然结论不成立,故A错误;
对于B,若b?β,显然结论不成立,故B错误;
对于C,以长方体ABCD-A′B′C′D′为例,AB∥平面A′B′C′D′,CD∥平面A′B′C′D′,BC⊥AB,BC⊥CD,
但BC与平面A′B′C′D′不垂直,故C错误;
对于D,由线面垂直的性质“垂直于同一个平面的两条直线平行“可知D正确.
故选:D.
点评 本题考查了空间线面位置关系的判断,借助几何模型举反例是关键,属于基础题.

练习册系列答案
相关题目
8.在等差数列{an}中,a3+a6=a4+5,且a2不大于1,则a8的取值范围是( )
| A. | (-∞,9] | B. | [9,+∞) | C. | (-∞,9) | D. | (9,+∞) |
18.双曲线$\frac{{x}^{2}}{16}$-$\frac{{y}^{2}}{4}$=1的左右焦点分别为F1、F2,点P为双曲线上任意一点,点Q是以点P为圆心,|PF1|为半径的圆上的任意点,那么|QF2|( )
| A. | 有最小值8 | B. | 有最大值8 | C. | 有最小值4$\sqrt{5}$ | D. | 有最大值4$\sqrt{5}$ |
2.双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的焦距为2c,直线l过点(a,0)和(0,b),且点($\frac{a}{2}$,0)到直线l的距离d≥$\frac{1}{5}$c,则双曲线的离心率e的取值范围是( )
| A. | [$\frac{3}{2}$,2] | B. | [$\frac{\sqrt{5}}{2}$,2] | C. | [$\frac{3}{2}$,$\sqrt{5}$] | D. | [$\frac{\sqrt{5}}{2}$,$\sqrt{5}$] |
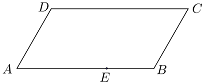 图为一块平行四边形园地ABCD,经测量,AB=20米,BC=10米,∠ABC=120°,拟过线段AB上一点E设计一条直路EF(点F在四边形ABCD的边上,不计路的宽度),将该园地分为面积之比为3:1的左、右两部分分别种植不同的花卉,设EB=x,EF=y(单位:米)
图为一块平行四边形园地ABCD,经测量,AB=20米,BC=10米,∠ABC=120°,拟过线段AB上一点E设计一条直路EF(点F在四边形ABCD的边上,不计路的宽度),将该园地分为面积之比为3:1的左、右两部分分别种植不同的花卉,设EB=x,EF=y(单位:米)