题目内容
(本小题满分14分)已知关于x的函数 .
.
(I)求函数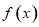 在点
在点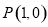 处的切线方程;
处的切线方程;
(II)求函数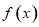 有极小值,试求a的取值范围;
有极小值,试求a的取值范围;
(III)若在区间 上,函数
上,函数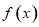 不出现在直线
不出现在直线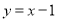 的上方,试求a的最大值.
的上方,试求a的最大值.
(Ⅰ)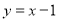 (Ⅱ)
(Ⅱ)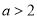 (III)
(III)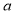 的最大值为0.
的最大值为0.
【解析】
试题分析:(Ⅰ)求导,利用导数的几何意义进行求解;(Ⅱ)求导,讨论二次方程的二次项系数的符号与两根的大小进行求解;(III)构造函数,将问题转化为不等式恒成立,利用导数求最值即可.
试题解析:(Ⅰ)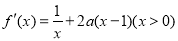
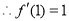
又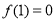
所以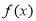 在点P(1,0)处的切线方程为
在点P(1,0)处的切线方程为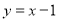 . 4分
. 4分
(Ⅱ)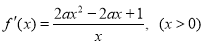 5分
5分
令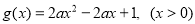
(i)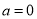 时
时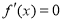 无解,
无解,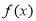 无极小值;
无极小值;
(ii) 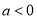 时,
时,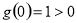 ,所以
,所以 有两解
有两解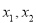 ,且
,且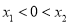 ;
;
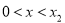 时
时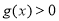 ,
,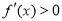
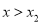 时
时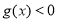 ,
,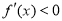
此时,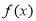 无极小值. 7分
无极小值. 7分
(iii) 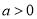 时, 因为
时, 因为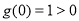 ,
,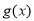 的对称轴为
的对称轴为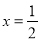 ,要使函数
,要使函数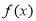 有极小值,则
有极小值,则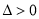 即
即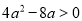
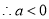 或
或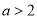
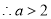
此时 有两解
有两解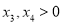 ,不妨设设
,不妨设设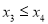 , 则
, 则 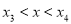 时
时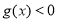 ,
,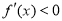
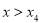 时
时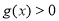 ,
,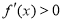 此时,
此时,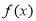 有极小值
有极小值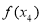 . 9分
. 9分
综上所述,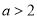 . 10分
. 10分
(Ⅲ)由题意,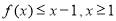
即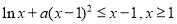 11分
11分
下证: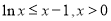
记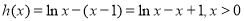
则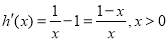
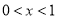 时
时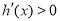 ,
,
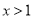 时
时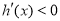 ,
,
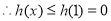
即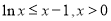 12分
12分
(i) 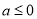 时,
时,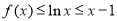
(ii) 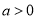 时,取
时,取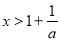 ,
,
则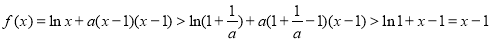
与题意矛盾.
故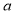 的最大值为0.
的最大值为0.
考点:1.导数的几何意义;2.函数的极值与最值;3.分类讨论思想.

练习册系列答案
 智慧小复习系列答案
智慧小复习系列答案
相关题目
 本不同的数学书和
本不同的数学书和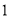 本语文书在书架上随机排成一行,则
本语文书在书架上随机排成一行,则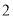 本数学书相邻的概率为
本数学书相邻的概率为 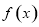 的定义域为
的定义域为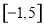 ,部分对应值如下表,
,部分对应值如下表,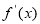 的图象如图所示.
的图象如图所示.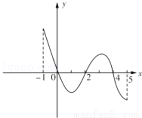
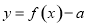 有
有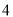 个零点,则实数
个零点,则实数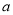 的取值范围为( )
的取值范围为( )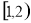 (B)
(B)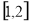 (C)
(C) 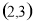 (D)
(D)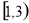

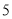 和
和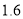 (B)
(B)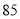 和
和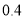 (D)
(D) 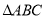 中,角A,B,C的对边分别为
中,角A,B,C的对边分别为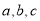 ,且
,且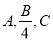 成等差数列.
成等差数列.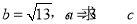 的值;
的值;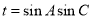 ,求t的最大值.
,求t的最大值. 图象的是
图象的是
 满足
满足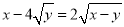 ,则
,则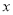 的取值范围是____________________.
的取值范围是____________________.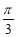 ,acosA=bcosB.
,acosA=bcosB.
