题目内容
(本小题满分12分)在 中,角A,B,C的对边分别为
中,角A,B,C的对边分别为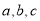 ,且
,且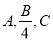 成等差数列.
成等差数列.
(I)若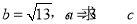 的值;
的值;
(II)设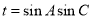 ,求t的最大值.
,求t的最大值.
(1) ;(2)
;(2) .
.
【解析】
试题分析:(1)利用等差中项和三角形的内角和定理得出角B,再利用余弦定理,得出关于 的方程进行求解;(2)将
的方程进行求解;(2)将 化成
化成 的形式,再利用三角函数的图像与性质进行求解.
的形式,再利用三角函数的图像与性质进行求解.
试题解析:(Ⅰ)因为 ,
, ,
, 成等差数列,
成等差数列,

因为 ,
,
所以 . 2分
. 2分
∵
 5分
5分
 6分
6分
(Ⅱ)∵
 10分
10分
∵ ,
,
 .
.
所以当 即
即 时,
时, 有最大值
有最大值 .
.
考点:1.等差数列;2.正弦定理;3.余弦定理;3.三角恒等变形;4.三角函数的图像与性质.

练习册系列答案
相关题目

 B.
B.  C.
C.  D.
D. 
 满足:
满足: .
. 的最小值
的最小值 ;
; ,对于(Ⅰ)中求得的
,对于(Ⅰ)中求得的 ,是否存在实数
,是否存在实数 使
使 成立,说明理由.
成立,说明理由. (其中
(其中 ),其部分图像如下图所示,将
),其部分图像如下图所示,将 的图像纵坐标不变,横坐标变成原来的2倍,再向右平移1个单位得到
的图像纵坐标不变,横坐标变成原来的2倍,再向右平移1个单位得到 的图像,则函数
的图像,则函数
 B.
B.
 D.
D.
 .
.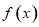 在点
在点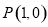 处的切线方程;
处的切线方程; 上,函数
上,函数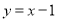 的上方,试求a的最大值.
的上方,试求a的最大值.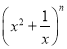 的二项展开式的各项系数和为32,则二项展开式中含
的二项展开式的各项系数和为32,则二项展开式中含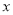 项的系数为________.
项的系数为________.
 B.
B.  C.
C.  D.
D. 
 在椭圆
在椭圆 上,
上, 为椭圆
为椭圆 的右焦点,若点
的右焦点,若点 满足
满足 且
且 ,则
,则 的最小值为( )
的最小值为( ) B.3 C.
B.3 C. D. 1
D. 1