题目内容
已知P是双曲线 的右支上一点,F1,F2分别为双曲线的左、右焦点,双曲线的离心率为e,下列命题正确的是( ).
的右支上一点,F1,F2分别为双曲线的左、右焦点,双曲线的离心率为e,下列命题正确的是( ).
A.双曲线的焦点到渐近线的距离为 ; ; |
B.若 ,则e的最大值为 ,则e的最大值为 ; ; |
| C.△PF1F2的内切圆的圆心的横坐标为a ; |
D.若∠F1PF2的外角平分线交x轴与M, 则 . . |
C
解析试题分析: 的焦点坐标为
的焦点坐标为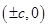 ,渐近线方程为
,渐近线方程为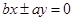 ,
,
对于选项A, 焦点到渐近线的距离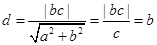 ,故A错;
,故A错;
对于选项B,设 ,若
,若 ,令
,令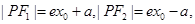 所以
所以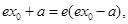 即
即 解得
解得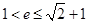 .故B错;
.故B错;
对于选项C:如图,设切点A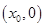 ,由切线长定理得:
,由切线长定理得: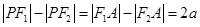 ,即
,即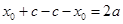 ,所以
,所以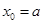 ,故△PF1F2的内切圆的圆心的横坐标为a,所以选项C正确
,故△PF1F2的内切圆的圆心的横坐标为a,所以选项C正确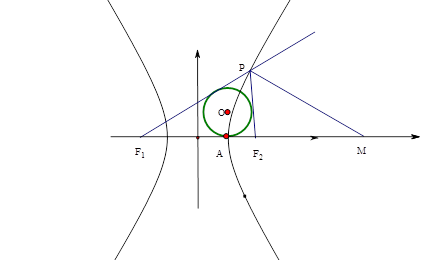
对于选项D:由外角平分线定理得: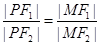
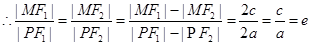 ,
,
故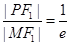 选项D错误,故选项为C..
选项D错误,故选项为C..
考点:渐近线方程;点到直线的距离公式;焦半径公式;外角平分线定理;合比定理.

练习册系列答案
 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案
相关题目
已知动点 在椭圆
在椭圆 上,若
上,若 点坐标为
点坐标为 ,
, ,且
,且 ,则
,则 的最小值是( )
的最小值是( )
A. | B. | C. | D. |
设 、
、 是关于
是关于 的方程
的方程 的两个不等实根,则过
的两个不等实根,则过 ,
, 两点的直线与双曲线
两点的直线与双曲线 的公共点的个数为( )
的公共点的个数为( )
| A.0 | B.1 | C.2 | D.3 |
从椭圆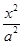 +
+ =1(a>b>0)上一点P向x轴作垂线,垂足恰为左焦点F1,A是椭圆与x轴正半轴的交点,B是椭圆与y轴正半轴的交点,且AB∥OP(O是坐标原点),则该椭圆的离心率是( )
=1(a>b>0)上一点P向x轴作垂线,垂足恰为左焦点F1,A是椭圆与x轴正半轴的交点,B是椭圆与y轴正半轴的交点,且AB∥OP(O是坐标原点),则该椭圆的离心率是( )
A. | B. | C. | D.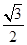 |
若椭圆 +
+ =1与双曲线
=1与双曲线 -
- =1(m,n,p,q均为正数)有共同的焦点F1,F2,P是两曲线的一个公共点,则
=1(m,n,p,q均为正数)有共同的焦点F1,F2,P是两曲线的一个公共点,则 ·
· =( )
=( )
| A.p2-m2 | B.p-m | C.m-p | D.m2-p2 |
 =1(a>0,b>0)的右焦点是抛物线y2=8x的焦点F,两曲线的一个公共点为P,且|PF| =5,则此双曲线的离心率为( )
=1(a>0,b>0)的右焦点是抛物线y2=8x的焦点F,两曲线的一个公共点为P,且|PF| =5,则此双曲线的离心率为( )


 与抛物线
与抛物线 有一个共同的焦点F, 点M是双曲线与抛物线的一个交点, 若
有一个共同的焦点F, 点M是双曲线与抛物线的一个交点, 若 , 则此双曲线的离心率等于( ).
, 则此双曲线的离心率等于( ).



 的两条渐近线与直线
的两条渐近线与直线 分别交于A,B两点,F为该双曲线的右焦点.若
分别交于A,B两点,F为该双曲线的右焦点.若 , 则该双曲线的离心率的取值范围是( )
, 则该双曲线的离心率的取值范围是( )


 -
- =1(a>0,b>0)的左,右焦点,若在双曲线右支上存在一点P,满足|PF2|=|F1F2|,且点F2到直线PF1的距离等于双曲线的实轴长,则该双曲线的离心率e为( )
=1(a>0,b>0)的左,右焦点,若在双曲线右支上存在一点P,满足|PF2|=|F1F2|,且点F2到直线PF1的距离等于双曲线的实轴长,则该双曲线的离心率e为( )

