题目内容
6.已知$\overrightarrow{m}$=$\overrightarrow{a}$+$\overrightarrow{b}$,$\overrightarrow{n}$=2$\overrightarrow{a}$+2$\overrightarrow{b}$($\overrightarrow{a}$,$\overrightarrow{b}$不共线),则$\overrightarrow{m}$与$\overrightarrow{n}$( )| A. | 共线 | B. | 不共线 | C. | 不共面 | D. | 以上都不对 |
分析 根据向量共线定理即可求出.
解答 解:∵$\overrightarrow{m}$=$\overrightarrow{a}$+$\overrightarrow{b}$,$\overrightarrow{n}$=2$\overrightarrow{a}$+2$\overrightarrow{b}$($\overrightarrow{a}$,$\overrightarrow{b}$不共线),
∴2$\overrightarrow{m}$=$\overrightarrow{n}$,
∴$\overrightarrow{m}$与$\overrightarrow{n}$共线,
故选:A
点评 本题考查了向量的共线定理,属于基础题.

练习册系列答案
相关题目
1.下列说法正确的是( )
| A. | 一个人打靶,打了10发子弹,有7发子弹中靶,因此这个人中靶的概率为0.7 | |
| B. | 一个同学做掷硬币试验,掷了6次,一定有3次“正面朝上” | |
| C. | 某地发行福利彩票,其回报率为47%,有个人花了100元钱买彩票,一定会有47元的回报 | |
| D. | 大量试验后,一个事件发生的频率在0.75附近波动,可以估计这个事件发生的概率为0.75 |
10. 如图,在直角梯形ABCD中,AB⊥AD,AB∥DC,AB=2,AD=DC=1,图中圆弧所在圆的圆心为点C,半径为$\frac{1}{2}$,且点P在图中阴影部分(包括边界)运动.若$\overrightarrow{AP}$=x$\overrightarrow{AB}$+y$\overrightarrow{BC}$,其中x,y∈R,则4x-y的取值范围是( )
如图,在直角梯形ABCD中,AB⊥AD,AB∥DC,AB=2,AD=DC=1,图中圆弧所在圆的圆心为点C,半径为$\frac{1}{2}$,且点P在图中阴影部分(包括边界)运动.若$\overrightarrow{AP}$=x$\overrightarrow{AB}$+y$\overrightarrow{BC}$,其中x,y∈R,则4x-y的取值范围是( )
 如图,在直角梯形ABCD中,AB⊥AD,AB∥DC,AB=2,AD=DC=1,图中圆弧所在圆的圆心为点C,半径为$\frac{1}{2}$,且点P在图中阴影部分(包括边界)运动.若$\overrightarrow{AP}$=x$\overrightarrow{AB}$+y$\overrightarrow{BC}$,其中x,y∈R,则4x-y的取值范围是( )
如图,在直角梯形ABCD中,AB⊥AD,AB∥DC,AB=2,AD=DC=1,图中圆弧所在圆的圆心为点C,半径为$\frac{1}{2}$,且点P在图中阴影部分(包括边界)运动.若$\overrightarrow{AP}$=x$\overrightarrow{AB}$+y$\overrightarrow{BC}$,其中x,y∈R,则4x-y的取值范围是( )| A. | $[2,\;\;3+\frac{{3\sqrt{2}}}{4}]$ | B. | $[2,\;\;3+\frac{{\sqrt{5}}}{2}]$ | ||
| C. | $[3-\;\;\frac{{\sqrt{2}}}{4},\;\;3+\frac{{\sqrt{5}}}{2}]$ | D. | $[3-\;\;\frac{{\sqrt{17}}}{2},\;\;3+\;\frac{{\sqrt{17}}}{2}]$ |
17.复数z=(a+1)+(a2-3)i,若z<0,则实数a的值是( )
| A. | $\sqrt{3}$ | B. | 1 | C. | -1 | D. | -$\sqrt{3}$ |
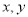 的值如下表所示,如果
的值如下表所示,如果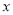 与
与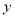 线性相关,且回归直线方程为
线性相关,且回归直线方程为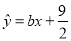 ,则实数
,则实数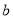 的值为( )
的值为( )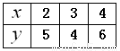
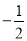 B.
B.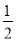 C.
C.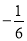 D.
D.