题目内容
2.已知函数f(x)=xlnx+ax(a∈R).(Ⅰ)若a=-2,求函数f(x)的单调区间;
(Ⅱ)若对任意x∈(1,+∞),f(x)>k(x-1)+ax-x恒成立,求正整数k的值.(参考数据:ln2=0.6931,ln3=1.0986)
分析 (I)利用导数判断f(x)的单调性和单调区间;
(II)分离参数得出k<$\frac{xlnx+x}{x-1}$,使用导数求出右侧函数的最小值,得出k的范围.
解答 解:(I)a=-2时,f(x)=xlnx-2x,则f′(x)=lnx-1.
令f′(x)=0得x=e,
当0<x<e时,f′(x)<0,当x>e时,f′(x)>0,
∴f(x)的单调递减区间是(0,e),单调递增区间为(e,+∞).
(II)若对任意x∈(1,+∞),f(x)>k(x-1)+ax-x恒成立,
则xlnx+ax>k(x-1)+ax-x恒成立,即k(x-1)<xlnx+ax-ax+x恒成立,
又x-1>0,则k<$\frac{xlnx+x}{x-1}$对任意x∈(1,+∞)恒成立,
设h(x)=$\frac{xlnx+x}{x-1}$,则h′(x)=$\frac{x-lnx-2}{(x-1)^{2}}$.
设m(x)=x-lnx-2,则m′(x)=1-$\frac{1}{x}$,
∵x∈(1,+∞),∴m′(x)>0,则m(x)在(1,+∞)上是增函数.
∵m(1)=-1<0,m(2)=-ln2<0,m(3)=1-ln3<0,m(4)=2-ln4>0,
∴存在x0∈(3,4),使得m(x0)=0,
当x∈(1,x0)时,m(x)<0,即h′(x)<0,
当x∈(x0,+∞)时,m(x)>0,h′(x)>0,
∴h(x)在(1,x0)上单调递减,在(x0,+∞)上单调递增,
∴h(x)的最小值hmin(x)=h(x0)=$\frac{{x}_{0}ln{x}_{0}+{x}_{0}}{{x}_{0}-1}$.
∵m(x0)=x0-lnx0-2=0,∴lnx0=x0-2.∴h(x0)=$\frac{{x}_{0}({x}_{0}-2)+{x}_{0}}{{x}_{0}-1}$=x0.
∴k<hmin(x)=x0.
∵3<x0<4,
∴k≤3.
∴k的值为1,2,3.
点评 本题考查了利用导数研究函数的单调性,函数的最值,函数恒成立问题,构造函数求出h(x)的最小值是解题关键,属于难题.

| A. | (-2,+∞) | B. | [-2,+∞) | C. | (-3,+∞) | D. | [-3,+∞) |
 ,求
,求 ( )
( )
 的直线与圆
的直线与圆 相切,则此直线在
相切,则此直线在 轴上的截距是
轴上的截距是 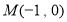 且斜率为
且斜率为 的直线与圆
的直线与圆 在第一象限内的部分有交点,则
在第一象限内的部分有交点,则 的取值范围是( )
的取值范围是( ) 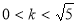 B.
B. C.
C. D.
D.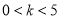
 在如图所示三棱锥D-ABC中,AD⊥DC,AB=4,AD=CD=2,∠BAC=45°,平面ACD⊥平面ABC,E,F分别在BD,BC,且BE=2ED,BC=2BF.
在如图所示三棱锥D-ABC中,AD⊥DC,AB=4,AD=CD=2,∠BAC=45°,平面ACD⊥平面ABC,E,F分别在BD,BC,且BE=2ED,BC=2BF.